Link classification
The links deposited in LinkProt database are divided into three categories:
- Deterministic links
- Probabilistic links
- Macromolecular links
In each category, the links are divided into topological classes and by the number of components which constitute the link. Each topological class is then subdivided into more exact subclasses taking into account also the
orientation and chirality of the link. The topological classification of each link type is described in this section. Currently the database collects information about links made of:
Among the complete protein structures (or when missing part of the protein chain does not change type of the topology) deposited in PDB we found 20 different types of links.
Deterministic links
Deterministic links are formed by covalent loops, closed by disulfide bridge. Such links can be inter- or intra-molecule (involving, respectively, one or more chains). The first one-chain links were identified in [1]. The only two-chain deterministic link was described in [2]. The LinkProt database automatically classifies both types of links. Currently, one- and two-chain deterministic links have been found.
The one- and two-chain deterministic links are classified into two main topological classes - Hopf ( ) and Solomon (
) and Solomon ( ) links. As the protein chain is naturally oriented from the N- to the C-terminus, the links formed by covalent loops are equipped with an inherited orientation. This, orientation in principle, splits the topological types into smaller, topologically distinct subgroups. In particular, in the case of one-chain links, one can distinguish three topological types: positive Hopf link, negative Hopf link, and negative Solomon link (Fig. 1). The Hopf link and the Solomon links are prime links found in the mathematical enumeration of links, while the composition (or connected sum) of the Solomon link and the Hopf link is not shown in the enumeration since the tables only list prime knots/links.
) links. As the protein chain is naturally oriented from the N- to the C-terminus, the links formed by covalent loops are equipped with an inherited orientation. This, orientation in principle, splits the topological types into smaller, topologically distinct subgroups. In particular, in the case of one-chain links, one can distinguish three topological types: positive Hopf link, negative Hopf link, and negative Solomon link (Fig. 1). The Hopf link and the Solomon links are prime links found in the mathematical enumeration of links, while the composition (or connected sum) of the Solomon link and the Hopf link is not shown in the enumeration since the tables only list prime knots/links.
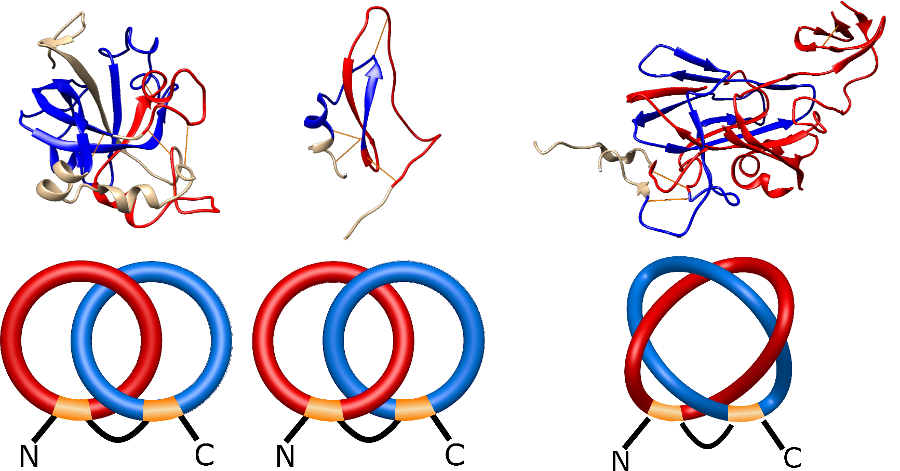
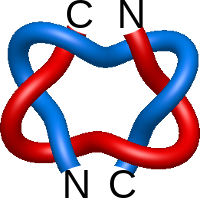
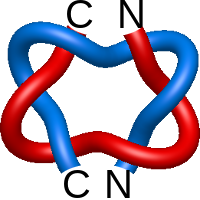
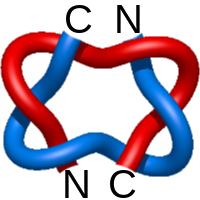
Fig. 1 Example structures with deterministic links within one chain (upper panel) with the topological schemae (bottom panel). From left to right, positive Hopf link (β-1,4-D-Endoglucanase with PDB code 1WC2), the negative Hopf link (Tick-derived Protease Inhibitor with PDB code 2LFK) and the negative Solomon link (flocculation protein with PDB code 2XJP). The covalent loops forming the link are depicted in red and blue, respectively. The orange segments denote the cysteine bridges.
On each covalent loop, a minimal surface is spanned (Fig. 2). This allows for the analysis of potentially biologically important amino acid residues actually piercing the spanning surface. Moreover, the chain orientation determines the surface orientation, and therefore the piercing direction. As a result, the chain orientation allows us also to prescribe a sign for Hopf and Solomon links - the signs are adjusted to match the sign of the piercings of the surface (determined as in [3]) spanning on the covalent loops and the other oriented component. For example, in case of the negative Hopf link, there is one piercing through each surface, and both piercings are negative.

Fig. 2 The surface spanning the covalent (linked) loops for the Epa1P protein with PDB code 4A3X. The left and right panels show surfaces spanning the individual loops, center panel - both surfaces shown together. To facilitate the view, the simplified, smoothed version of protein is depicted (as in [3]).
Two-chain deterministic links are exceptionally rare. They consist of two topological classes - the positive Hopf link and the positive Solomon link. The two-chain positive Hopf link is seen in citrate sythase [2] (Fig. 3). The low number of two-component deterministic links indicates that the formation of such structures is less probable. No three-chain deterministic link have been found to date.
The two-chain deterministic links are analyzed in the same manner as one-chain links. In particular the LinkProt database assigns a minimal surface to each covalent loop and calculates the surface piercings (Fig. 3). A rotating depiction of the protein can be viewed at the top of the page.
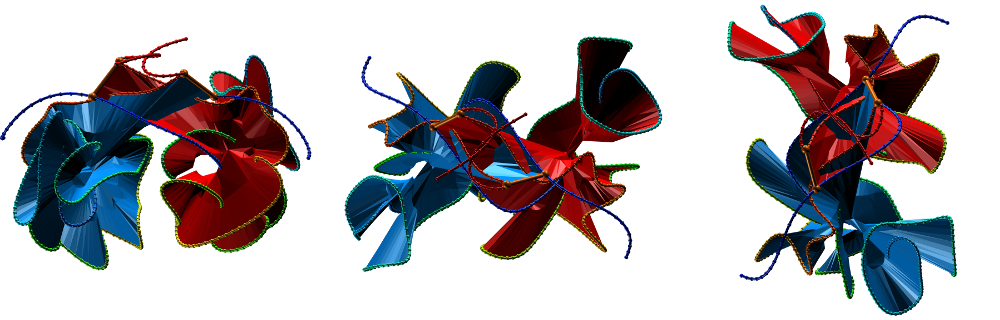
Fig. 3 Citrate syntase with PDB code 2IBP [2] with both surface spanned, seen in different projections.
The probabilistic links
In probabilistic links, the link components are formed by entire chains, closed at infinity (as in the case of defining the closure for knotted proteins [4]), described in greater detail in the link detection section. Because of the definition, such links can only be formed by two or more chains. Since, in principle, the link type depends on the closure direction, the link type is calculated for many closure directions and the total likelihood variation of the associated topological link types is presented for each protein. Moreover, the user has the possibility to define the cut-off likelihood for which the structures will be displayed. In fact, there are only a few structures for which the likelihood of link formation is greater than 60%, and all of these structures are Hopf link structures (either positive or negative). With decreasing the likelihood cut-off, more structures and more topological motifs are present. In particular, for a likelihood cut-off of 10%, in addition to the Hopf link models, there are also Solomon links, the David star, and two-eights-link proteins. We would like to stress that for a low likelihood cut-off, some proteins may be present simultaneously in different topological groups. For example, the Poliovirus late rna-release intermediate with PDB code 3IYC has the likelihood of Solomon link equal ca. 15% (so it would be displayed in Solomon link group for a cut-off lower than 15%), but it is also likely to be seen as a Hopf-link protein (the likelihood equal ca 34%). The default likelihood cut-off is set at 30%. The most common two-chain probabilistic links are presented in Tab. 1. Similar to the deterministic links, the LinkProt server also takes into account the orientation of the chains, which splits the possible topological type into subtypes. Currently, the LinkProt uses the HOMFLY-PT polynomial to identify all prime two-component links up to 14 crossings in their minimal crossing representation and most component links up to 8 crossings. Including three- and four-chain structures, polynomials for almost 24.000 structures were calculated. Nevertheless, for some structures, there occur topological classes named "other" reflecting the presence of chains that form exceptionally complicated links. Such structures will be progressively identified and added to the database.
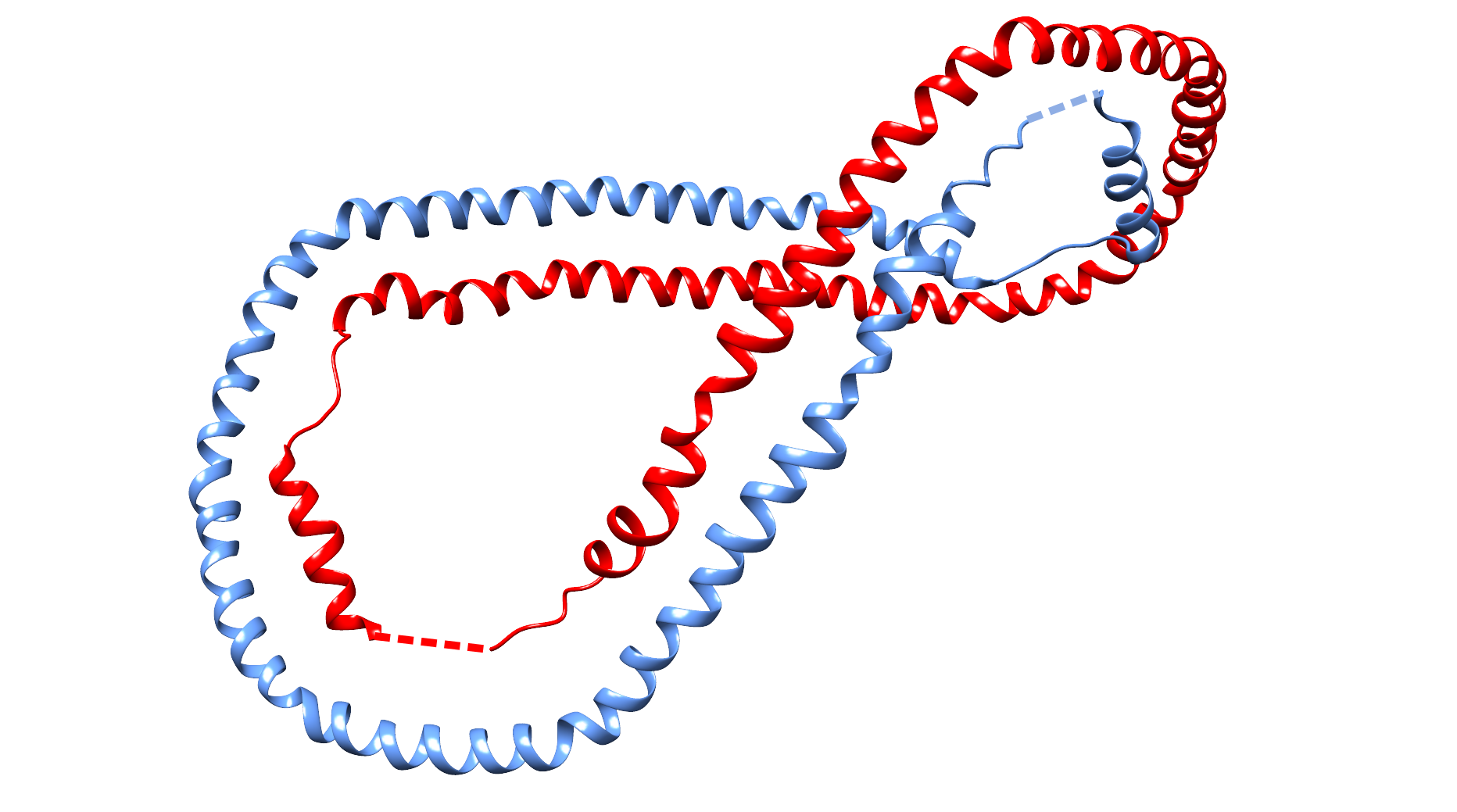
Fig. 4 Exemplary structure of human apolipoprotein a-i (PDB code 1AV1) with high probability of Hopf link structure. The chain termini were joined by straight, dashed interval.
All the two-chain links with probability greater or equall to 10% are presented in Tab. 1. Similarly to the "Search" page, clicking on each link class will display subclasses of two-component links identified so far. Below the table there is a list of other two-chain links identified, which were not assinged 10% in any case. For each link the relevant HOMFLY-PT polynomial is shown.
In the case of three chain structures, additional links are possible. These are mainly composition of two Hopf links (one ring joining two others -  ), the
), the  link (
link ( ), in which each two components form the Hopf link, and a Hopf link with a split circle (
), in which each two components form the Hopf link, and a Hopf link with a split circle ( ). Such structures are presented in Tab. 2. All the probabilistic links are treated in the same manner as deterministic links for each chain termini connection. In particular, for each termini connection, the LinkProt database assigns a (triangulated) minimal surface and counts its piercings (Fig. 4).
). Such structures are presented in Tab. 2. All the probabilistic links are treated in the same manner as deterministic links for each chain termini connection. In particular, for each termini connection, the LinkProt database assigns a (triangulated) minimal surface and counts its piercings (Fig. 4).

Fig. 5 The exemplary surfaces spanning three component protein probabilistic links.
All the three-chain links with probability greater or equall to 10% are presented in Tab. 2. Similarly to the "Search" page, clicking on each link class will display subclasses of three-component links identified so far. Below the table there is a list of other three-chain links identified, which were not assinged 10% in any case. For each link the relevant HOMFLY-PT polynomial is shown.

Fig. 5 The exemplary surfaces spanning three component protein probabilistic links.
All the three-chain links with probability greater or equall to 10% are presented in Tab. 2. Similarly to the "Search" page, clicking on each link class will display subclasses of three-component links identified so far. Below the table there is a list of other three-chain links identified, which were not assinged 10% in any case. For each link the relevant HOMFLY-PT polynomial is shown.
The four-component links are builed mainly as a split sum of two- or three-component links with a suitable number of rings (Hopf U 2 Rings, Hopf # Hopf U Ring or Solomon # Hopf U Ring). Nevertheless, in the case of Crystal structure of human apolipoprotein a-i there is 20% probability of a four-component link with at least 12 crossing in minimal corssing representation. As such links were not named officially, we call that particular link (distinguished by its HOMFLY-PT polynomial) L12n1. We however do not claim, that it is 12 crossing link (although it seems so).
The possible four-component links with at least 10% probability are given in the Tab. 3. In case of four-component links, there is however much higher dependence of link type on the direction of termini extensio
n. Therefore the Table of other found links, with probability less than 10% can be also useful. Such table, with relevant HOMFLY-PT polynomials is given below Tab. 3.
Macromolecular links
In the structure of Bordetella bacteriophage BBP-1 (PDB code: 3J4U) there is a "chainmail" structure that was first identified in [5]. In the head of BBP-1, there are major capsid proteins (MCP) and 'cement proteins' (CP) that decorate the shell. However, there was no clear description of how the proteins in the head of BBP-1 are linked. We fill this gap by classifying these links.
The macromolecular links are formed by closed loops which are defined by connecting chains in the macromolecular structure. Currently, LinkProt contains 4 types of Macromolecular links in MCP. In each of the components, the orientation is clock-wise, and the closure of the components is made by connecting chains in the natural order of the amino acids:
- The simplest example is a Hopf link, which has a positive sign if we take into account the order of the amino acids (the sign depends on the arrangements of the components). Neighboring polygons (these can be pentagons or hexagons) form Hopf links.
- When we go one level higher, i.e. considering three component links, the
 link with 6 crossings is formed (found also for three chain probabilistic links). It is distinguished from other links with 3 components links with six crossing by the fact that it is non-alternating - as one follows a component of the link, the crossings do not always alternate between over and under crossings. Each pair of the components is a positive Hopf link.
link with 6 crossings is formed (found also for three chain probabilistic links). It is distinguished from other links with 3 components links with six crossing by the fact that it is non-alternating - as one follows a component of the link, the crossings do not always alternate between over and under crossings. Each pair of the components is a positive Hopf link.
It is also possible to consider links with a larger number of components. Such is the case with the flower link. It is composed of a central component, surrounded by other components - facets. Each of the facets forms a positive Hopf with the central component as do any two neighboring facets. There are two types of flower links with:
- the central component being a pentagon - it has 20 crossings,
- the central component being a hexagon - it has 24 crossings.
More generally, the flower link with an n-polygon in the center has 4n crossings. In general, the macromolecular link found in Bordetella bacteriophage BBP-1 has the multi-level link structure presented in the Fig. 6.
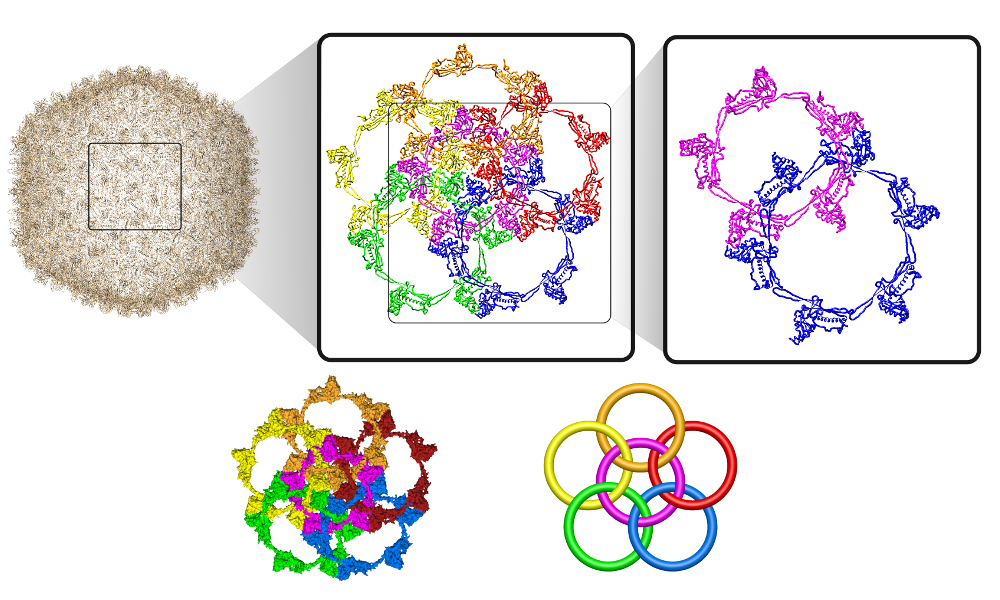
Fig. 6 The multilevel link structure of Bordetella bacteriophage BBP-1 (top panel) with the simplified depiction of the flower link (bottom panel).
Link tables
Below we present the tables containing links with probability equal or greater then 10 for two-, three-, and four-component links. For each link number of distinct subtypes (taking into account the chirality and orientation) both theoretically possible and observed (with at least 10% probability) is given. The difference of these numbers is the number of missing subclasses. Clicking on each row sho
ws observed subclasses with their representative structures and HOMFLY-PT polynomial. Below each table one can click on the "Show observed structures with less then 10% probability" to find examples of other links stored in LinkProt database.
Two-component links
Show observed structures with less then 10% probability.
| Link type |
Image |
HOMFLY-PT polynomial |
Example |
 |
 |
=m^{-1}(l^{7}+5 l^{5}+8 l^{3}+4 l)-m(4 l+10 l^{3}+6 l^{5}+l^{7}) + m^3(l+5 l^{3}+2 l^{5})-m^{5}l^{3}) |
crystal structure of tyrosine aminotransferase tripple mutant (p181q, 2 r183g,a321k) from escherichia coli at 2.35 a resolution |
 |
 |
=m^{-1}(2l^{-5}+7l^{-3}+7l^{-1}+2l)-m(l^{-5}+7l^{-3}+10l^{-1}+3l)+m^{3}(2l^{-3}+5l^{-1}+l)-m^{5}l) |
met94thr/phe312cys variant of nitrite reductase from 2 alcaligenes faecalis |
 |
 |
=m^{-1}(l^{-11}+5l^{-9}+8l^{-7}+4l^{-5})-m(3l^{-9}+10l^{-7}+8l^{-5})+m^{3}(3l^{-7}+5l^{-5})-m^{5}l^{-5}) |
crystal structure of chemically synthesized [aib51/51']hiv-1 protease |
 |
 |
=m^{-1}(4 l^{5}+8 l^{7}+5 l^{9}+l^{11})-m(8 l^{5}+10 l^{7}+3l^{9})+m^{3}(5 l^{5}+3 l^{7}+5 l^{9})-m^{5}l^{5}) |
structure of glutamate dehydrogenase complexed with 2 bithionol |
 |
 |
=m^{-1}(2l^{-1}+7 l+7 l^{3}+2 l^{5})-m(3l^{-1}+10 l+7 l^{3}+l^{5})+m^3(l^{-1}+5 l+2 l^{3})-m^{5}l) |
met62leu variant of nitrite reductase from alcaligenes 2 faeclis |
 |
 |
=m^{-1}(l^{-7}+5l^{-5}+8l^{-3}+4l^{-1})-m(l^{-7}+6l^{-5}+10l^{-3}+4l^{-1})+m^{3}(2l^{-5}+5l^{-3}+l^{-1})-m^{5}l^{-3}) |
the 1.4 a crystal structure of the large and cold-active 2 vibrio sp. alkaline phosphatase |
 |
 |
=-m^{-1}(2l^{-1}+5 l+6 l^{3}+4 l^{5}+l^{7})+m(l^{-1}+4 l+5 l^{3}+2 l^{5})-m^{3}(l+l^{3})) |
crystal structure of trichoderma reesei aspartic proteinase complexed 2 with pepstatin a |
 |
 |
=l^{3} m - \frac{l^{3}}{m} - l m^{3} + 3 l m - \frac{3 l}{m} + \frac{m}{l} - \frac{2}{l m}) |
crystal structure of snx9px-bar (230-595), h32 |
 |
 |
=\frac{1}{m} \left(- \frac{2}{l^{3}} - \frac{3}{l^{5}} - \frac{1}{l^{7}}\right) - \frac{m^{3}}{l^{3}} + \frac{3 m}{l^{3}} + \frac{2 m}{l^{5}}) |
sec61 in the canine ribosome-channel complex from the 2 endoplasmic reticulum |
 |
 |
=2 l^{5} m - l^{3} m^{3} + 3 l^{3} m + \frac{1}{m} \left(- l^{7} - 3 l^{5} - 2 l^{3}\right)) |
crystal structure of tyrosine aminotransferase tripple mutant (p181q, 2 r183g,a321k) from escherichia coli at 2.35 a resolution |
 |
 |
=l m + \frac{1}{m} \left(- 2 l - \frac{3}{l} - \frac{1}{l^{3}}\right) - \frac{m^{3}}{l} + \frac{3 m}{l} + \frac{m}{l^{3}}) |
crystal structure of the first active autolysate form of 2 the porcine alpha trypsin |
 |
 |
=- \frac{l^{9}}{m} + 2 l^{7} m - \frac{5 l^{7}}{m} - l^{5} m^{3} + 6 l^{5} m - \frac{8 l^{5}}{m} - l^{3} m^{3} + 4 l^{3} m - \frac{4 l^{3}}{m}) |
crystal structure of the chimeric muscarinic toxin mt7 with loop 1 2 from mt1. |
 |
 |
=l^{3} m - \frac{2 l^{3}}{m} - l m^{3} + 5 l m - \frac{7 l}{m} - \frac{m^{3}}{l} + \frac{5 m}{l} - \frac{7}{l m} + \frac{m}{l^{3}} - \frac{2}{l^{3} m}) |
crystal structure of e. coli nadp dependent enzyme |
 |
 |
=- \frac{m^{3}}{l^{3}} + \frac{4 m}{l^{3}} - \frac{4}{l^{3} m} - \frac{m^{3}}{l^{5}} + \frac{6 m}{l^{5}} - \frac{8}{l^{5} m} + \frac{2 m}{l^{7}} - \frac{5}{l^{7} m} - \frac{1}{l^{9} m}) |
hiv protease inhibitors with pseudo-symmetric cores |
 |
 |
=- \frac{l^{7}}{m} + 2 l^{5} m - \frac{4 l^{5}}{m} - l^{3} m^{3} + 5 l^{3} m - \frac{6 l^{3}}{m} - l m^{3} + 4 l m - \frac{5 l}{m} + \frac{m}{l} - \frac{2}{l m}) |
poliovirus late rna-release intermediate |
 |
 |
=l m - \frac{2 l}{m} - \frac{m^{3}}{l} + \frac{4 m}{l} - \frac{5}{l m} - \frac{m^{3}}{l^{3}} + \frac{5 m}{l^{3}} - \frac{6}{l^{3} m} + \frac{2 m}{l^{5}} - \frac{4}{l^{5} m} - \frac{1}{l^{7} m}) |
crystal structure of the sodium-potassium pump |
 |
 |
=\frac{l^{11}}{m} - 2 l^{9} m + \frac{4 l^{9}}{m} + l^{7} m^{3} - 4 l^{7} m + \frac{4 l^{7}}{m} + l^{5} m - \frac{l^{5}}{m} - l^{3} m^{3} + 3 l^{3} m - \frac{2 l^{3}}{m}) |
vp7 recoated rotavirus dlp |
 |
 |
=- l^{5} m + \frac{2 l^{5}}{m} + l^{3} m^{3} - 4 l^{3} m + \frac{5 l^{3}}{m} - l m + \frac{2 l}{m} - \frac{m^{3}}{l} + \frac{3 m}{l} - \frac{2}{l m} + \frac{m}{l^{3}} - \frac{1}{l^{3} m}) |
the 1.8 angstrom crystal structure of the dimeric 2 peroxisomal thiolase of saccharomyces cerevisiae |
 |
 |
=- \frac{m^{3}}{l^{3}} + \frac{3 m}{l^{3}} - \frac{2}{l^{3} m} + \frac{m}{l^{5}} - \frac{1}{l^{5} m} + \frac{m^{3}}{l^{7}} - \frac{4 m}{l^{7}} + \frac{4}{l^{7} m} - \frac{2 m}{l^{9}} + \frac{4}{l^{9} m} + \frac{1}{l^{11} m}) |
hiv pr drug resistant patient's variant in complex with darunavir |
 |
 |
=- l^{3} m + \frac{2 l^{3}}{m} + l m^{3} - 4 l m + \frac{5 l}{m} - \frac{2 m}{l} + \frac{4}{l m} - \frac{m^{3}}{l^{3}} + \frac{3 m}{l^{3}} - \frac{1}{l^{3} m} + \frac{2 m}{l^{5}} - \frac{3}{l^{5} m} - \frac{1}{l^{7} m}) |
the crystal structure of the narghi mutant narh - c16a |
 |
 |
=l m + \frac{1}{m} \left(- l - \frac{2}{l} - \frac{2}{l^{3}} - \frac{1}{l^{5}}\right) - \frac{m^{3}}{l} + \frac{2 m}{l} + \frac{2 m}{l^{3}}) |
crystal structure of blub-like flavoprotein (yp_001089088.1) from 2 clostridium difficile 630 at 1.74 a resolution |
 |
 |
=2 l^{3} m - l m^{3} + 2 l m + \frac{1}{m} \left(- l^{5} - 2 l^{3} - 2 l - \frac{1}{l}\right) + \frac{m}{l}) |
crystal structures of escherichia coli aspartate 2 aminotransferase in two conformations: comparison of an 3 unliganded open and two liganded closed forms |
 |
 |
=- \frac{l^{5}}{m} + 2 l^{3} m - \frac{3 l^{3}}{m} - l m^{3} + 4 l m - \frac{5 l}{m} - \frac{m^{3}}{l} + \frac{4 m}{l} - \frac{5}{l m} + \frac{2 m}{l^{3}} - \frac{3}{l^{3} m} - \frac{1}{l^{5} m}) |
hiv-1 protease mutant g86a with symmetric inhibitor dmp323 |
 |
 |
=\frac{l^{9}}{m} - 2 l^{7} m + \frac{3 l^{7}}{m} + l^{5} m^{3} - 3 l^{5} m + \frac{3 l^{5}}{m} + \frac{l^{3}}{m} - l m^{3} + 2 l m - \frac{l}{m} + \frac{m}{l} - \frac{1}{l m}) |
aspartate aminotransferase hexamutant |
 |
 |
=l m - \frac{l}{m} - \frac{m^{3}}{l} + \frac{2 m}{l} - \frac{1}{l m} + \frac{1}{l^{3} m} + \frac{m^{3}}{l^{5}} - \frac{3 m}{l^{5}} + \frac{3}{l^{5} m} - \frac{2 m}{l^{7}} + \frac{3}{l^{7} m} + \frac{1}{l^{9} m}) |
crystal structure of uncomplexed hiv_1 protease subtype a |
 |
 |
=- l m + \frac{1}{m} \left(l^{3} + 2 l + \frac{2}{l} + \frac{1}{l^{3}}\right) - \frac{m}{l}) |
hiv-1 protease mutant g86a with symmetric inhibitor dmp323 |
 |
 |
=l^{7} m - \frac{2 l^{7}}{m} - l^{5} m^{3} + 5 l^{5} m - \frac{5 l^{5}}{m} - l^{3} m^{3} + 4 l^{3} m - \frac{3 l^{3}}{m}) |
crystal structure of the bacteriophage phi29 gene product 12 c- 2 terminal fragment |
 |
 |
=- \frac{m^{3}}{l^{3}} + \frac{4 m}{l^{3}} - \frac{3}{l^{3} m} - \frac{m^{3}}{l^{5}} + \frac{5 m}{l^{5}} - \frac{5}{l^{5} m} + \frac{m}{l^{7}} - \frac{2}{l^{7} m}) |
alkaline phosphatase (d153h, k328h) |
 |
 |
=- l^{5} m + \frac{l^{5}}{m} + l^{3} m^{3} - 2 l^{3} m + \frac{2 l^{3}}{m} - l m^{3} + l m + \frac{m}{l} - \frac{1}{l m}) |
catalase a from saccharomyces cerevisiae |
 |
 |
=- \frac{m^{3}}{l^{3}} + \frac{2 m}{l^{3}} - \frac{1}{l^{3} m} + \frac{m^{3}}{l^{5}} - \frac{m}{l^{5}} - \frac{2 m}{l^{7}} + \frac{2}{l^{7} m} + \frac{1}{l^{9} m}) |
crystal structure of uncomplexed hiv_1 protease subtype a |
 |
 |
=\frac{l^{9}}{m} - 2 l^{7} m + \frac{2 l^{7}}{m} + l^{5} m^{3} - l^{5} m - l^{3} m^{3} + 2 l^{3} m - \frac{l^{3}}{m}) |
poliovirus early rna-release intermediate |
 |
 |
=l m - \frac{l}{m} - \frac{m^{3}}{l} + \frac{m}{l} + \frac{m^{3}}{l^{3}} - \frac{2 m}{l^{3}} + \frac{2}{l^{3} m} - \frac{m}{l^{5}} + \frac{1}{l^{5} m}) |
hiv pr drug resistant patient's variant in complex with darunavir |
 |
 |
=- \frac{l^{7}}{m} + l^{5} m - \frac{2 l^{5}}{m} - l m + \frac{l}{m}) |
crystal structure of the bacteriophage phi29 gene product 12 c- 2 terminal fragment |
 |
 |
=- \frac{m}{l} + \frac{1}{l m} + \frac{m}{l^{5}} - \frac{2}{l^{5} m} - \frac{1}{l^{7} m}) |
a complex of extracellular domain of tissue factor with an 2 inhibitory fab (5g9) |
 |
 |
=l m - \frac{l}{m} - \frac{m^{3}}{l} + \frac{m}{l} - \frac{1}{l m} + \frac{m^{3}}{l^{3}} - \frac{m}{l^{3}} + \frac{1}{l^{3} m} - \frac{2 m}{l^{5}} + \frac{2}{l^{5} m} + \frac{1}{l^{7} m}) |
the crystal structure of the narghi mutant narh - c16a |
 |
 |
=\frac{l^{7}}{m} - 2 l^{5} m + \frac{2 l^{5}}{m} + l^{3} m^{3} - l^{3} m + \frac{l^{3}}{m} - l m^{3} + l m - \frac{l}{m} + \frac{m}{l} - \frac{1}{l m}) |
crystal structure of a ntf2-like protein (ava_2261) from anabaena 2 variabilis atcc 29413 at 1.65 a resolution revdat 3 28-jul-10 3dmc 1 header keywds |
 |
 |
=- \frac{l^{5}}{m} + 2 l^{3} m - \frac{l^{3}}{m} - l m^{3} + \frac{l}{m} + \frac{m^{3}}{l} - \frac{2 m}{l} + \frac{2}{l m} - \frac{m}{l^{3}} + \frac{1}{l^{3} m}) |
the crystal structure of the narghi mutant narh - c16a |
 |
 |
=- \frac{l^{5}}{m} + l^{3} m - \frac{2 l^{3}}{m} - \frac{l}{m} - \frac{m}{l} + \frac{1}{l m} + \frac{1}{l^{3} m}) |
the crystal structure of the narghi mutant narh - c16a |
 |
 |
=\frac{l^{3}}{m} - l m + \frac{l}{m} - \frac{1}{l m} + \frac{m}{l^{3}} - \frac{2}{l^{3} m} - \frac{1}{l^{5} m}) |
the crystal structure of the narghi mutant narh - c16a |
 |
 |
=m^{-1}(l^{-7}+l^{-5})-m(l^{-7}+2l^{-5}-2l^{-3})+m^3(l^{-5}-l^{-3})) |
domain swapping of staphylococcus aureus thioredoxin w28a 2 mutant |
 |
 |
=m^{-1}(l^{5}+l^{7})+m(2l^{3}-2l^{5}-l^{7})-m^3(l^{3}-l^{5})) |
crystal structure of cyanovirin-n complexed to oligomannose-9 (man-9) |
 |
 |
=-m^{-1}(l^{3}+l^{5})+m(l^{-1}+l^{1}+2l^{3})-ml) |
crystal structure of cyanovirin-n complexed to oligomannose-9 (man-9) |
 |
 |
=-m^{-1}(l^{-5}+l^{-3})-m(l^{-7}+l^{-5}-2l^{-3})+m(l^{-5}-l^{-3})) |
catalase a from saccharomyces cerevisiae |
 |
 |
=-m^{-1}(l^{-5}+l^{-3})+m(2l^{-3}+l^{-1}+l^{1})-ml^{-1}) |
gramicidin d from bacillus brevis (ethanol solvate) |
 |
 |
=-m^{-1}(l^{3}+l^{5})+m(2l^{3}-l^{5}-l^{7})-m(l^{3}-l^{5})) |
poliovirus late rna-release intermediate |
 |
 |
=\frac{1}{m} \left(\frac{1}{l} + \frac{1}{l^{3}}\right) + \frac{m^{3}}{l} - \frac{3 m}{l} - \frac{m^{5}}{l^{3}} + \frac{4 m^{3}}{l^{3}} - \frac{4 m}{l^{3}} + \frac{m^{3}}{l^{5}} - \frac{2 m}{l^{5}}) |
poliovirus late rna-release intermediate |
 |
 |
=- l^{3} m + l m^{3} - 2 l m + \frac{1}{m} \left(l^{3} + l\right) - \frac{m^{3}}{l} + \frac{m}{l} + \frac{m}{l^{3}}) |
gramicidin d from bacillus brevis (methanol solvate) |
 |
 |
=l^{5} m^{3} - 2 l^{5} m - l^{3} m^{5} + 4 l^{3} m^{3} - 4 l^{3} m + l m^{3} - 3 l m + \frac{1}{m} \left(l^{3} + l\right)) |
crystal structure of e. coli nadp dependent enzyme |
 |
 |
=l^{3} m - l m^{3} + l m + \frac{1}{m} \left(\frac{1}{l} + \frac{1}{l^{3}}\right) + \frac{m^{3}}{l} - \frac{2 m}{l} - \frac{m}{l^{3}}) |
ribonuclease inhibitor-angiogenin complex |
 |
 |
=l^{3} m^{3} - 2 l^{3} m - l m^{5} + 4 l m^{3} - 5 l m + \frac{1}{m} \left(l^{3} + l\right) + \frac{m^{3}}{l} - \frac{2 m}{l}) |
crystal structure of amprenavir (apv) in complex with a drug resistant 2 hiv-1 protease variant (i50l/a71v). |
 |
 |
=l m + \frac{1}{m} \left(\frac{1}{l} + \frac{1}{l^{3}}\right) - \frac{m^{3}}{l} + \frac{m^{3}}{l^{3}} - \frac{m}{l^{3}} - \frac{m}{l^{5}}) |
crystal structure of tyrosine aminotransferase tripple mutant (p181q, 2 r183g,a321k) from escherichia coli at 2.35 a resolution |
 |
 |
=l m^{3} - 2 l m + \frac{1}{m} \left(\frac{1}{l} + \frac{1}{l^{3}}\right) - \frac{m^{5}}{l} + \frac{4 m^{3}}{l} - \frac{5 m}{l} + \frac{m^{3}}{l^{3}} - \frac{2 m}{l^{3}}) |
structural basis for specificity of retroviral proteases |
 |
 |
=- l^{5} m + l^{3} m^{3} - l^{3} m - l m^{3} + \frac{1}{m} \left(l^{3} + l\right) + \frac{m}{l}) |
hiv-1 protease mutant g86s with darunavir |
 |
 |
=l m + \frac{1}{m} \left(- l - \frac{1}{l}\right) - \frac{m^{3}}{l} + \frac{m}{l} + \frac{m^{3}}{l^{3}} - \frac{m}{l^{3}} - \frac{m}{l^{5}}) |
crystal structure of the minor histocompatibility peptide 2 ha-1his in complex with hla-a2 |
 |
 |
=- l^{5} m + l^{3} m^{3} - l^{3} m - l m^{3} + l m + \frac{1}{m} \left(- l - \frac{1}{l}\right) + \frac{m}{l}) |
hiv-1 protease mutant g86s with darunavir |
 |
 |
=l^{5} m^{3} - 2 l^{5} m - l^{3} m^{5} + 4 l^{3} m^{3} - 5 l^{3} m + l m^{3} - 3 l m + \frac{1}{m} \left(l^{5} + 3 l^{3} + 2 l\right)) |
crystal structure of chemically synthesized [d-ala51/51']hiv-1 2 protease |
 |
 |
={m^{3}}{l} - \frac{3 m}{l} - \frac{m^{5}}{l^{3}} + \frac{4 m^{3}}{l^{3}} - \frac{5 m}{l^{3}} + \frac{m^{3}}{l^{5}} - \frac{2 m}{l^{5}}) |
crystal structure of tyrosine aminotransferase tripple mutant (p181q, 2 r183g,a321k) from escherichia coli at 2.35 a resolution |
 |
 |
=\frac{1}{m} \left(\frac{2}{l^{5}} + \frac{3}{l^{7}} + \frac{1}{l^{9}}\right) - \frac{m^{3}}{l^{3}} + \frac{m}{l^{3}} + \frac{2 m^{3}}{l^{5}} - \frac{4 m}{l^{5}} - \frac{3 m}{l^{7}}) |
crystal structure of cyanovirin-n complexed to oligomannose-9 (man-9) |
 |
 |
=l^{3} m^{3} - 2 l^{3} m - l m^{5} + 4 l m^{3} - 6 l m + \frac{1}{m} \left(2 l^{3} + 3 l + \frac{1}{l}\right) + \frac{m^{3}}{l} - \frac{2 m}{l}) |
met62leu variant of nitrite reductase from alcaligenes 2 faeclis |
 |
 |
=- 3 l^{7} m + 2 l^{5} m^{3} - 4 l^{5} m - l^{3} m^{3} + l^{3} m + \frac{1}{m} \left(l^{9} + 3 l^{7} + 2 l^{5}\right)) |
hiv pr drug resistant patient's variant in complex with darunavir |
 |
 |
=frac{m^{5}}{l} + \frac{4 m^{3}}{l} - \frac{6 m}{l} + \frac{m^{3}}{l^{3}} - \frac{2 m}{l^{3}}) |
crystal structure of hla-b*2709 complexed with the double 2 citrullinated vasoactive intestinal peptide type 1 receptor 3 (vipr) peptide (residues 400-408) |
 |
 |
=l m^{3} - l m + \frac{1}{m} \left(- l - \frac{1}{l}\right) - \frac{m^{5}}{l} + \frac{3 m^{3}}{l} - \frac{2 m}{l} + \frac{m^{3}}{l^{3}} - \frac{m}{l^{3}}) |
phosphorylation of self-peptides alters human leukocyte antigen class 2 i-restricted antigen presentation and generates tumor specific 3 epitopes |
 |
 |
=l^{3} m^{3} - l^{3} m - l m^{5} + 3 l m^{3} - 2 l m + \frac{1}{m} \left(- l - \frac{1}{l}\right) + \frac{m^{3}}{l} - \frac{m}{l}) |
crystal structure of tyrosine aminotransferase tripple mutant (p181q, 2 r183g,a321k) from escherichia coli at 2.35 a resolution |
 |
 |
=- l m + \frac{1}{m} \left(l + \frac{3}{l} + \frac{2}{l^{3}}\right) + \frac{m^{3}}{l} - \frac{4 m}{l} - \frac{m}{l^{3}}) |
crystal structure of b*4405 presenting a 10mer ebv epitope |
 |
 |
=- l^{3} m + l m^{3} - 4 l m + \frac{1}{m} \left(2 l^{3} + 3 l + \frac{1}{l}\right) - \frac{m}{l}) |
catalase a from saccharomyces cerevisiae |
 |
 |
=\frac{1}{m} \left(\frac{2}{l} + \frac{3}{l^{3}} + \frac{1}{l^{5}}\right) - \frac{2 m}{l} + \frac{m^{3}}{l^{3}} - \frac{3 m}{l^{3}} - \frac{m}{l^{5}}) |
poliovirus early rna-release intermediate |
 |
 |
=- l^{5} m + l^{3} m^{3} - 3 l^{3} m - 2 l m + \frac{1}{m} \left(l^{5} + 3 l^{3} + 2 l\right)) |
crystal structure of the inhibitor atazanavir (atv) in complex with a 2 multi-drug resistance hiv-1 protease variant 3 (l10i/g48v/i54v/v64i/v82a) refer: flap+ in citation. |
 |
 |
=l^{3} m^{3} - l^{3} m - l m^{5} + 3 l m^{3} - 4 l m + \frac{1}{m} \left(l^{3} + 2 l + \frac{2}{l} + \frac{1}{l^{3}}\right) + \frac{2 m^{3}}{l} - \frac{4 m}{l} - \frac{m}{l^{3}}) |
kcsa potassium channel in the partially open state with 14.5 a opening 2 at t112 |
 |
 |
=- l^{3} m + 2 l m^{3} - 4 l m + \frac{1}{m} \left(l^{3} + 2 l + \frac{2}{l} + \frac{1}{l^{3}}\right) - \frac{m^{5}}{l} + \frac{3 m^{3}}{l} - \frac{4 m}{l} + \frac{m^{3}}{l^{3}} - \frac{m}{l^{3}}) |
crystal structure of the binary complex between hla-a2 and 2 hcmv nlv-m5q peptide variant |
 |
 |
=l^{7} m - l^{5} m + l^{3} m - l m + \frac{1}{m} \left(- l^{9} - l^{7}\right)) |
universal stress protein tead from the trap transporter teaabc of 2 halomonas elongata |
 |
 |
=- l^{9} m^{3} + l^{9} m + l^{7} m^{5} - 2 l^{7} m^{3} - 2 l^{7} m - l^{5} m^{5} + 4 l^{5} m^{3} - 5 l^{5} m + \frac{1}{m} \left(l^{9} + 3 l^{7} + 2 l^{5}\right)) |
poliovirus early rna-release intermediate |
 |
 |
=frac{m^{5}}{l^{5}} + \frac{4 m^{3}}{l^{5}} - \frac{5 m}{l^{5}} + \frac{m^{5}}{l^{7}} - \frac{2 m^{3}}{l^{7}} - \frac{2 m}{l^{7}} - \frac{m^{3}}{l^{9}} + \frac{m}{l^{9}}) |
crystal structure of protease inhibitor, ad78 in complex with wild 2 type hiv-1 protease |
 |
 |
=- l^{3} m + 2 l m^{3} - 5 l m + \frac{1}{m} \left(2 l^{3} + 3 l + \frac{1}{l}\right) - \frac{m^{5}}{l} + \frac{3 m^{3}}{l} - \frac{3 m}{l} + \frac{m^{3}}{l^{3}} - \frac{m}{l^{3}}) |
poliovirus early rna-release intermediate |
 |
 |
=\frac{1}{m} \left(- \frac{1}{l^{7}} - \frac{1}{l^{9}}\right) - \frac{m^{7}}{l^{7}} + \frac{7 m^{5}}{l^{7}} - \frac{15 m^{3}}{l^{7}} + \frac{10 m}{l^{7}} + \frac{m^{5}}{l^{9}} - \frac{5 m^{3}}{l^{9}} + \frac{6 m}{l^{9}}) |
structural basis for the autoregulation of the zinc 2 transporter yiip |
 |
 |
=l m^{3} - l m + \frac{1}{m} \left(\frac{2}{l} + \frac{3}{l^{3}} + \frac{1}{l^{5}}\right) - \frac{m^{5}}{l} + \frac{3 m^{3}}{l} - \frac{4 m}{l} + \frac{2 m^{3}}{l^{3}} - \frac{4 m}{l^{3}} - \frac{m}{l^{5}}) |
human class i mhc hla-a2(a150p) in complex with the tax peptide |
 |
 |
=l m^{3} + \frac{1}{m} \left(- l - \frac{1}{l}\right) - \frac{m^{5}}{l} + \frac{2 m^{3}}{l} - \frac{m}{l} + \frac{2 m^{3}}{l^{3}} - \frac{2 m}{l^{3}} - \frac{m}{l^{5}}) |
crystal structure of a ntf2-like protein (ava_2261) from anabaena 2 variabilis atcc 29413 at 1.65 a resolution revdat 3 28-jul-10 3dmc 1 header keywds |
 |
 |
=- 2 l m + \frac{1}{m} \left(l^{3} + 2 l + \frac{2}{l} + \frac{1}{l^{3}}\right) + \frac{m^{3}}{l} - \frac{3 m}{l} - \frac{m}{l^{3}}) |
hiv-1 protease mutant g86a with darunavir |
 |
 |
=- l^{3} m + l m^{3} - 3 l m + \frac{1}{m} \left(l^{3} + 2 l + \frac{2}{l} + \frac{1}{l^{3}}\right) - \frac{2 m}{l}) |
hiv-1 protease mutant g86a with symmetric inhibitor dmp323 |
 |
 |
=l^{5} m^{3} - 3 l^{5} m - l^{3} m^{5} + 4 l^{3} m^{3} - 4 l^{3} m + l m^{3} - 3 l m + \frac{1}{m} \left(l^{7} + 2 l^{5} + 2 l^{3} + l\right)) |
crystal structures of escherichia coli aspartate aminotransferase in 2 two conformations: comparison of an unliganded open and two liganded 3 closed forms |
 |
 |
=\frac{1}{m} \left(\frac{1}{l} + \frac{2}{l^{3}} + \frac{2}{l^{5}} + \frac{1}{l^{7}}\right) - \frac{2 m}{l} + \frac{m^{3}}{l^{3}} - \frac{2 m}{l^{3}} - \frac{2 m}{l^{5}}) |
catalase a from saccharomyces cerevisiae |
 |
 |
=\frac{1}{m} \left(\frac{1}{l} + \frac{2}{l^{3}} + \frac{2}{l^{5}} + \frac{1}{l^{7}}\right) + \frac{m^{3}}{l} - \frac{3 m}{l} - \frac{m^{5}}{l^{3}} + \frac{4 m^{3}}{l^{3}} - \frac{4 m}{l^{3}} + \frac{m^{3}}{l^{5}} - \frac{3 m}{l^{5}}) |
crystal structure of wild type hiv-1 protease with novel p1'-ligand 2 grl-02031 |
 |
 |
=- 2 l^{5} m + l^{3} m^{3} - 2 l^{3} m - 2 l m + \frac{1}{m} \left(l^{7} + 2 l^{5} + 2 l^{3} + l\right)) |
poliovirus late rna-release intermediate |
 |
 |
=- l^{9} m^{3} + 3 l^{9} m + l^{7} m^{5} - 4 l^{7} m^{3} + 4 l^{7} m - l^{5} m^{5} + 4 l^{5} m^{3} - 3 l^{5} m + \frac{1}{m} \left(- l^{9} - l^{7}\right)) |
crystal structure of cyanovirin-n complexed to oligomannose-9 (man-9) |
 |
 |
=\frac{1}{m} \left(- \frac{1}{l^{7}} - \frac{1}{l^{9}}\right) - \frac{m^{3}}{l^{3}} + \frac{2 m}{l^{3}} + \frac{m^{3}}{l^{5}} - \frac{m}{l^{5}} - \frac{m^{3}}{l^{7}} + \frac{2 m}{l^{7}} + \frac{m}{l^{9}}) |
kcsa potassium channel in the partially open state with 16 a opening 2 at t112 |
 |
 |
=\frac{1}{m} \left(- \frac{1}{l^{7}} - \frac{1}{l^{9}}\right) - \frac{m^{5}}{l^{5}} + \frac{4 m^{3}}{l^{5}} - \frac{3 m}{l^{5}} + \frac{m^{5}}{l^{7}} - \frac{4 m^{3}}{l^{7}} + \frac{4 m}{l^{7}} - \frac{m^{3}}{l^{9}} + \frac{3 m}{l^{9}}) |
catalase a from saccharomyces cerevisiae |
 |
 |
=l^{9} m - l^{7} m^{3} + 2 l^{7} m + l^{5} m^{3} - l^{5} m - l^{3} m^{3} + 2 l^{3} m + \frac{1}{m} \left(- l^{9} - l^{7}\right)) |
hiv-1 protease mutant g86s with darunavir |
 |
 |
=\frac{1}{m} \left(\frac{1}{l^{5}} + \frac{1}{l^{7}}\right) - \frac{m^{5}}{l^{5}} + \frac{4 m^{3}}{l^{5}} - \frac{4 m}{l^{5}} + \frac{m^{5}}{l^{7}} - \frac{3 m^{3}}{l^{7}} + \frac{m}{l^{7}} - \frac{m^{3}}{l^{9}} + \frac{2 m}{l^{9}}) |
crystal structure of protease inhibitor, ad78 in complex with wild 2 type hiv-1 protease |
 |
 |
=- 2 l^{5} m + l^{3} m^{3} - l m^{3} + \frac{1}{m} \left(l^{7} + l^{5}\right) + \frac{m}{l}) |
hiv-1 protease mutant g86s with darunavir |
 |
 |
=- l^{9} m^{3} + 2 l^{9} m + l^{7} m^{5} - 3 l^{7} m^{3} + l^{7} m - l^{5} m^{5} + 4 l^{5} m^{3} - 4 l^{5} m + \frac{1}{m} \left(l^{7} + l^{5}\right)) |
crystal structures of escherichia coli aspartate aminotransferase in 2 two conformations: comparison of an unliganded open and two liganded 3 closed forms |
 |
 |
=l m + \frac{1}{m} \left(\frac{1}{l^{5}} + \frac{1}{l^{7}}\right) - \frac{m^{3}}{l} + \frac{m^{3}}{l^{3}} - \frac{2 m}{l^{5}}) |
rabbit muscle l-lactate dehydrogenase in complex with nadh and oxamate |
 |
 |
=\frac{1}{m} \left(- \frac{1}{l^{7}} - \frac{1}{l^{9}}\right) - \frac{m^{5}}{l^{5}} + \frac{4 m^{3}}{l^{5}} - \frac{4 m}{l^{5}} + \frac{m^{5}}{l^{7}} - \frac{3 m^{3}}{l^{7}} + \frac{2 m}{l^{7}} - \frac{m^{3}}{l^{9}} + \frac{2 m}{l^{9}}) |
structure of rotavirus outer capsid protein vp7 trimer in complex with 2 a neutralizing fab |
 |
 |
=\frac{1}{m} \left(- \frac{1}{l^{7}} - \frac{1}{l^{9}}\right) - \frac{m^{3}}{l^{3}} + \frac{m}{l^{3}} + \frac{2 m^{3}}{l^{5}} - \frac{3 m}{l^{5}} - \frac{m^{3}}{l^{7}} + \frac{m}{l^{7}} + \frac{m}{l^{9}}) |
the active site of yeast aspartyl-trna synthetase: 2 structural and functional aspects of the aminoacylation 3 reaction |
 |
 |
=- l^{9} m^{3} + 2 l^{9} m + l^{7} m^{5} - 3 l^{7} m^{3} + 2 l^{7} m - l^{5} m^{5} + 4 l^{5} m^{3} - 4 l^{5} m + \frac{1}{m} \left(- l^{9} - l^{7}\right)) |
crystal structure of a ntf2-like protein (ava_2261) from anabaena 2 variabilis atcc 29413 at 1.65 a resolution revdat 3 28-jul-10 3dmc 1 header keywds |
 |
 |
=\frac{1}{m} \left(\frac{1}{l^{5}} + \frac{1}{l^{7}}\right) - \frac{m^{3}}{l^{3}} + \frac{m}{l^{3}} + \frac{2 m^{3}}{l^{5}} - \frac{3 m}{l^{5}} - \frac{m^{3}}{l^{7}} + \frac{m}{l^{9}}) |
catalase a from saccharomyces cerevisiae |
 |
 |
=- l^{7} m + 2 l^{5} m^{3} - 4 l^{5} m - l^{3} m^{5} + 3 l^{3} m^{3} - 2 l^{3} m + l m^{3} - 2 l m + \frac{1}{m} \left(l^{7} + l^{5}\right)) |
crystal structure of e. coli nadp dependent enzyme |
 |
 |
=l^{9} m - l^{7} m^{3} + 2 l^{5} m^{3} - 3 l^{5} m - l^{3} m^{3} + l^{3} m + \frac{1}{m} \left(l^{7} + l^{5}\right)) |
structural basis for the catalytic activity of aspartate 2 aminotransferase k258h lacking the pyridoxal-5'-phosphate binding 3 lysine residue |
 |
 |
=\frac{1}{m} \left(\frac{1}{l^{5}} + \frac{1}{l^{7}}\right) + \frac{m^{3}}{l} - \frac{2 m}{l} - \frac{m^{5}}{l^{3}} + \frac{3 m^{3}}{l^{3}} - \frac{2 m}{l^{3}} + \frac{2 m^{3}}{l^{5}} - \frac{4 m}{l^{5}} - \frac{m}{l^{7}}) |
kcsa e71h-f103a mutant in the closed state |
 |
 |
=\frac{1}{m} \left(- \frac{1}{l^{3}} - \frac{1}{l^{5}}\right) - \frac{m^{3}}{l^{3}} + \frac{2 m}{l^{3}} + \frac{m^{3}}{l^{5}} - \frac{m^{3}}{l^{7}} + \frac{m}{l^{7}} + \frac{m}{l^{9}}) |
crystal structure of uncomplexed hiv_1 protease subtype a |
 |
 |
=2 l^{3} m - l m^{3} + \frac{1}{m} \left(- l^{5} - l^{3}\right) + \frac{m^{3}}{l} - \frac{m}{l} - \frac{m}{l^{3}}) |
betaine aldehyde dehydrogenase from cod liver |
 |
 |
=l^{9} m - l^{7} m^{3} + l^{7} m + l^{5} m^{3} - l^{3} m^{3} + 2 l^{3} m + \frac{1}{m} \left(- l^{5} - l^{3}\right)) |
crystal structure of tyrosine aminotransferase tripple mutant (p181q, 2 r183g,a321k) from escherichia coli at 2.35 a resolution |
 |
 |
=- l^{3} m + l m^{3} - l m + \frac{1}{m} \left(- \frac{1}{l^{3}} - \frac{1}{l^{5}}\right) - \frac{m^{3}}{l} + \frac{2 m}{l^{3}}) |
crystal structure of the bacteriophage phi29 gene product 12 c- 2 terminal fragment |
 |
 |
=- l^{3} m + 2 l m^{3} - 4 l m + \frac{1}{m} \left(l^{3} + l\right) - \frac{m^{5}}{l} + \frac{3 m^{3}}{l} - \frac{3 m}{l} + \frac{m^{3}}{l^{3}} - \frac{m}{l^{3}}) |
crystal structure of the sodium-potassium pump |
 |
 |
=\frac{1}{m} \left(\frac{1}{l} + \frac{1}{l^{3}}\right) + \frac{m^{3}}{l} - \frac{2 m}{l} - \frac{m^{5}}{l^{3}} + \frac{3 m^{3}}{l^{3}} - \frac{3 m}{l^{3}} + \frac{2 m^{3}}{l^{5}} - \frac{3 m}{l^{5}} - \frac{m}{l^{7}}) |
hiv pr drug resistant patient's variant in complex with darunavir |
 |
 |
=l^{3} m^{3} - l^{3} m - l m^{5} + 3 l m^{3} - 3 l m + \frac{1}{m} \left(\frac{1}{l} + \frac{1}{l^{3}}\right) + \frac{2 m^{3}}{l} - \frac{4 m}{l} - \frac{m}{l^{3}}) |
met62leu variant of nitrite reductase from alcaligenes 2 faeclis |
 |
 |
=- l^{7} m + 2 l^{5} m^{3} - 3 l^{5} m - l^{3} m^{5} + 3 l^{3} m^{3} - 3 l^{3} m + l m^{3} - 2 l m + \frac{1}{m} \left(l^{3} + l\right)) |
crystal structures of escherichia coli aspartate aminotransferase in 2 two conformations: comparison of an unliganded open and two liganded 3 closed forms |
 |
 |
=l m^{3} - l m + \frac{1}{m} \left(\frac{1}{l} + \frac{1}{l^{3}}\right) - \frac{m^{5}}{l} + \frac{3 m^{3}}{l} - \frac{4 m}{l} + \frac{2 m^{3}}{l^{3}} - \frac{3 m}{l^{3}} - \frac{m}{l^{5}}) |
catalase a from saccharomyces cerevisiae |
 |
 |
=- l^{5} m + 2 l^{3} m^{3} - 3 l^{3} m - l m^{5} + 3 l m^{3} - 4 l m + \frac{1}{m} \left(l^{3} + l\right) + \frac{m^{3}}{l} - \frac{m}{l}) |
leishmania tarentolae mitochondrial large ribosomal subunit 2 model |
 |
 |
=- l^{7} m + 2 l^{5} m^{3} - 4 l^{5} m - l^{3} m^{5} + 3 l^{3} m^{3} - 3 l^{3} m + l m^{3} - 2 l m + \frac{1}{m} \left(l^{7} + 2 l^{5} + 2 l^{3} + l\right)) |
crystal structure of trichoderma reesei aspartic proteinase complexed 2 with pepstatin a |
 |
 |
=\frac{1}{m} \left(\frac{1}{l} + \frac{2}{l^{3}} + \frac{2}{l^{5}} + \frac{1}{l^{7}}\right) + \frac{m^{3}}{l} - \frac{2 m}{l} - \frac{m^{5}}{l^{3}} + \frac{3 m^{3}}{l^{3}} - \frac{3 m}{l^{3}} + \frac{2 m^{3}}{l^{5}} - \frac{4 m}{l^{5}} - \frac{m}{l^{7}}) |
catalase a from saccharomyces cerevisiae |
 |
 |
=l^{3} m - l m^{3} + \frac{1}{m} \left(l^{3} + l\right) + \frac{m^{3}}{l} - \frac{m}{l} - \frac{m}{l^{3}}) |
kcsa potassium channel in the partially open state with 14.5 a opening 2 at t112 |
Star of David.1
 |
 |
=m^{-1}(l^{-7}+l^{-5})-3m(l^{-7}+2l^{-5})+m^3(5l^{-5}+l^{-7})-ml^{-5}) |
kinetics and crystal structure of a mutant e. coli alkaline 2 phosphatase (asp-369-->asn): a mechanism involving one 3 zinc per active site |
Star of David.2
 |
 |
=m^{-1}(l^{5}+l^{7})-m(l-l^{3}+l^{5})) |
ribonuclease inhibitor-angiogenin complex |
Star of David.3
 |
 |
=m^{-1}(l^{5}+l^{7})-3m(2l^{5}+l^{7})+m^3(5l^{5}+l^7)-ml^{5}) |
poliovirus late rna-release intermediate |
Whitehead.1
 |
 |
=m^{-1}(l^{-1}+l^{1})+m(l^{-3}+2l^{-1}+l)-ml^{-1}) |
crystal structure of aahiv, a metalloproteinase from venom of 2 agkistrodon acutus |
Whitehead.2
 |
 |
=m^{-1}(l^{-1}+l^{1})+m(l^{-1}+2l^{1}+l^{3})-ml) |
aspartate aminotransferase, w140h mutant, maleate complex |
Three-component links
Show observed structures with less then 10% probability.
| Link type |
Image |
HOMFLY-PT polynomial |
Example |
 |
 |
=l^{6} - \frac{l^{6}}{m^{2}} - 2 l^{4} m^{2} + 5 l^{4} - \frac{4 l^{4}}{m^{2}} + l^{2} m^{4} - 4 l^{2} m^{2} + 7 l^{2} - \frac{5 l^{2}}{m^{2}} - m^{2} + 3 - \frac{2}{m^{2}}) |
crystal structure of e. coli nadp dependent enzyme |
 |
 |
=- l^{4} - 4 l^{2} + m^{2} \left(l^{2} + 1\right) - 4 + \frac{1}{m^{2}} \left(l^{4} + 4 l^{2} + 5 + \frac{2}{l^{2}}\right) - \frac{1}{l^{2}}) |
copper amine oxidase from hansenula polymorpha |
 |
 |
=m^{2} \left(\frac{1}{l^{2}} + \frac{1}{l^{4}}\right) + \frac{1}{m^{2}} \left(\frac{2}{l^{2}} + \frac{5}{l^{4}} + \frac{4}{l^{6}} + \frac{1}{l^{8}}\right) - \frac{3}{l^{2}} - \frac{5}{l^{4}} - \frac{2}{l^{6}}) |
crystal structure of adenylylsulfate reductase from 2 desulfovibrio gigas |
 |
 |
=- 2 l^{6} - 5 l^{4} - 3 l^{2} + m^{2} \left(l^{4} + l^{2}\right) + \frac{1}{m^{2}} \left(l^{8} + 4 l^{6} + 5 l^{4} + 2 l^{2}\right)) |
met62leu variant of nitrite reductase from alcaligenes 2 faeclis |
 |
 |
=- l^{2} + m^{2} \left(1 + \frac{1}{l^{2}}\right) - 4 + \frac{1}{m^{2}} \left(2 l^{2} + 5 + \frac{4}{l^{2}} + \frac{1}{l^{4}}\right) - \frac{4}{l^{2}} - \frac{1}{l^{4}}) |
crystal structure of adenylylsulfate reductase from 2 desulfovibrio gigas |
 |
 |
=m^{2} \left(-1 - \frac{4}{l^{2}} - \frac{2}{l^{4}}\right) + 3 + \frac{1}{m^{2}} \left(-2 - \frac{5}{l^{2}} - \frac{4}{l^{4}} - \frac{1}{l^{6}}\right) + \frac{m^{4}}{l^{2}} + \frac{7}{l^{2}} + \frac{5}{l^{4}} + \frac{1}{l^{6}}) |
crystal structure of adenylylsulfate reductase from 2 desulfovibrio gigas |
 |
 |
=l^{4} + 2 l^{2} + 1 + \frac{1}{m^{2}} \left(- l^{6} - 4 l^{4} - 5 l^{2} - 2\right)) |
crystal structure of blub-like flavoprotein (yp_001089088.1) from 2 clostridium difficile 630 at 1.74 a resolution |
 |
 |
=m \left(l + \frac{2}{l} + \frac{2}{l^{3}}\right) + \frac{1}{m} \left(- l - \frac{2}{l} - \frac{2}{l^{3}} - \frac{1}{l^{5}}\right) - \frac{m^{3}}{l}) |
crystal structure of blub-like flavoprotein (yp_001089088.1) from 2 clostridium difficile 630 at 1.74 a resolution |
 |
 |
=- l m^{3} + m \left(2 l^{3} + 2 l + \frac{1}{l}\right) + \frac{1}{m} \left(- l^{5} - 2 l^{3} - 2 l - \frac{1}{l}\right)) |
crystal structure of dnr from pseudomonas aeruginosa. |
 |
 |
=l^{2} + 2 + \frac{1}{m^{2}} \left(- l^{4} - 3 l^{2} - 4 - \frac{3}{l^{2}} - \frac{1}{l^{4}}\right) + \frac{1}{l^{2}}) |
secreted aspartic protease 1 from candida parapsilosis in complex with 2 pepstatin a |
 |
 |
=- l^{8} - 6 l^{6} - 9 l^{4} - 4 l^{2} + m^{2} \left(l^{6} + 2 l^{4} + l^{2}\right) + \frac{1}{m^{2}} \left(2 l^{8} + 7 l^{6} + 8 l^{4} + 3 l^{2}\right)) |
lidless mm-cpn in the closed state with atp/alfx |
 |
 |
=m^{2} \left(\frac{1}{l^{2}} - \frac{1}{l^{6}}\right) + \frac{1}{m^{2}} \left(- \frac{1}{l^{4}} - \frac{2}{l^{6}} - \frac{1}{l^{8}}\right) - \frac{2}{l^{2}} + \frac{3}{l^{6}} + \frac{1}{l^{8}}) |
refinement of the influenza virus hemagglutinin by simulated annealing |
 |
 |
=l^{8} + 3 l^{6} - 2 l^{2} + m^{2} \left(- l^{6} + l^{2}\right) + \frac{1}{m^{2}} \left(- l^{8} - 2 l^{6} - l^{4}\right)) |
crystal structure of archaeal 20s proteasome in complex with 2 mutated p26 activator |
 |
 |
=m^{2} \left(\frac{1}{l^{2}} - \frac{1}{l^{6}}\right) + \frac{1}{m^{2}} \left(\frac{1}{l^{2}} + \frac{2}{l^{4}} + \frac{1}{l^{6}}\right) - \frac{2}{l^{2}} - \frac{1}{l^{4}} + \frac{2}{l^{6}} + \frac{1}{l^{8}}) |
refinement of the influenza virus hemagglutinin by simulated annealing |
 |
 |
=- l^{2} + m^{2} \left(1 + \frac{1}{l^{2}}\right) - 2 + \frac{1}{m^{2}} \left(\frac{1}{l^{2}} + \frac{2}{l^{4}} + \frac{1}{l^{6}}\right) - \frac{3}{l^{2}} - \frac{2}{l^{4}}) |
copper amine oxidase from hansenula polymorpha |
 |
 |
=l^{8} + 2 l^{6} - l^{4} - 2 l^{2} + m^{2} \left(- l^{6} + l^{2}\right) + \frac{1}{m^{2}} \left(l^{6} + 2 l^{4} + l^{2}\right)) |
crystal structure of tyrosine aminotransferase tripple mutant (p181q, 2 r183g,a321k) from escherichia coli at 2.35 a resolution |
 |
 |
=- 2 l^{4} - 3 l^{2} + m^{2} \left(l^{2} + 1\right) - 2 + \frac{1}{m^{2}} \left(l^{6} + 2 l^{4} + l^{2}\right) - \frac{1}{l^{2}}) |
crystal structure of adenylylsulfate reductase from 2 desulfovibrio gigas |
 |
 |
=l^{4} + l^{2} m^{4} + 3 l^{2} + m^{2} \left(- l^{4} - 3 l^{2} - 1\right) + 2 + \frac{1}{m^{2}} \left(- l^{4} - 2 l^{2} - 1\right)) |
crystal structure of human apolipoprotein a-i |
 |
 |
=l^{4} + l^{2} m^{4} + 3 l^{2} + m^{2} \left(- l^{4} - 3 l^{2} - 1\right) + 2 + \frac{1}{m^{2}} \left(- l^{4} - 2 l^{2} - 1\right)) |
crystal structure of e. coli nadp dependent enzyme |
 |
 |
=l^{4} + l^{2} m^{4} + 3 l^{2} + m^{2} \left(- l^{4} - 3 l^{2} - 1\right) + 2 + \frac{1}{m^{2}} \left(- l^{4} - 2 l^{2} - 1\right)) |
refinement of the influenza virus hemagglutinin by simulated annealing |
 |
 |
=l^{4} + l^{2} m^{4} + 3 l^{2} + m^{2} \left(- l^{4} - 3 l^{2} - 1\right) + 2 + \frac{1}{m^{2}} \left(- l^{4} - 2 l^{2} - 1\right)) |
cystal structure of rhesus macaque mhc class i:mamu-a*02 |
 |
 |
=m^{4} + m^{2} \left(- l^{2} - 2 - \frac{1}{l^{2}}\right) + \frac{1}{m^{2}} \left(l^{2} + 2 + \frac{1}{l^{2}}\right)) |
crystal structure of e. coli nadp dependent enzyme |
 |
 |
=2 + \frac{1}{m^{2}} \left(-1 - \frac{2}{l^{2}} - \frac{1}{l^{4}}\right) - \frac{m^{2}}{l^{2}} + \frac{3}{l^{2}} + \frac{1}{l^{4}}) |
coiled-coil domain of tumor susceptibility gene 101 |
 |
 |
=m^{4} \left(\frac{1}{l^{2}} + \frac{1}{l^{4}}\right) + m^{2} \left(-1 - \frac{5}{l^{2}} - \frac{5}{l^{4}} - \frac{1}{l^{6}}\right) + 3 + \frac{1}{m^{2}} \left(-1 - \frac{2}{l^{2}} - \frac{1}{l^{4}}\right) + \frac{7}{l^{2}} + \frac{6}{l^{4}} + \frac{2}{l^{6}}) |
crystal structure of the sodium-potassium pump |
 |
 |
=l^{4} + 3 l^{2} + m^{2} \left(- l^{2} + \frac{1}{l^{2}}\right) + 1 + \frac{1}{m^{2}} \left(- l^{4} - 2 l^{2} - 1\right) - \frac{2}{l^{2}} - \frac{1}{l^{4}}) |
ribonuclease inhibitor-angiogenin complex |
 |
 |
=2 l^{6} + 6 l^{4} + 7 l^{2} + m^{4} \left(l^{4} + l^{2}\right) + m^{2} \left(- l^{6} - 5 l^{4} - 5 l^{2} - 1\right) + 3 + \frac{1}{m^{2}} \left(- l^{4} - 2 l^{2} - 1\right)) |
cystal structure of rhesus macaque mhc class i:mamu-a*02 |
 |
 |
=- l^{4} - 2 l^{2} + m^{2} \left(l^{2} - \frac{1}{l^{2}}\right) + 1 + \frac{1}{m^{2}} \left(-1 - \frac{2}{l^{2}} - \frac{1}{l^{4}}\right) + \frac{3}{l^{2}} + \frac{1}{l^{4}}) |
crystal structure of e. coli nadp dependent enzyme |
 |
 |
=2 l^{4} + 7 l^{2} + m^{4} \left(l^{2} + 1\right) + m^{2} \left(- l^{4} - 5 l^{2} - 5 - \frac{1}{l^{2}}\right) + 7 + \frac{1}{m^{2}} \left(- l^{4} - 2 l^{2} - 1\right) + \frac{2}{l^{2}}) |
cystal structure of rhesus macaque mhc class i:mamu-a*02 |
 |
 |
=- l^{2} + m^{2} \left(1 - \frac{1}{l^{4}}\right) - 1 + \frac{1}{m^{2}} \left(-1 - \frac{2}{l^{2}} - \frac{1}{l^{4}}\right) + \frac{1}{l^{2}} + \frac{2}{l^{4}} + \frac{1}{l^{6}}) |
crystal structure of tyrosine aminotransferase tripple mutant (p181q, 2 r183g,a321k) from escherichia coli at 2.35 a resolution |
 |
 |
=2 l^{2} + m^{4} \left(1 + \frac{1}{l^{2}}\right) + m^{2} \left(- l^{2} - 5 - \frac{5}{l^{2}} - \frac{1}{l^{4}}\right) + 7 + \frac{1}{m^{2}} \left(-1 - \frac{2}{l^{2}} - \frac{1}{l^{4}}\right) + \frac{7}{l^{2}} + \frac{2}{l^{4}}) |
crystal structure of blub-like flavoprotein (yp_001089088.1) from 2 clostridium difficile 630 at 1.74 a resolution |
 |
 |
=l^{6} + 2 l^{4} + l^{2} + m^{2} \left(- l^{4} + 1\right) - 1 + \frac{1}{m^{2}} \left(- l^{4} - 2 l^{2} - 1\right) - \frac{1}{l^{2}}) |
crystal structure of adenylylsulfate reductase from 2 desulfovibrio gigas |
 |
 |
=- l^{2} + m^{2} \left(1 - \frac{1}{l^{4}}\right) - 2 + \frac{1}{m^{2}} \left(l^{2} + 2 + \frac{1}{l^{2}}\right) + \frac{2}{l^{4}} + \frac{1}{l^{6}}) |
lidless mm-cpn in the closed state with atp/alfx |
 |
 |
=l^{6} + 2 l^{4} + m^{2} \left(- l^{4} + 1\right) - 2 + \frac{1}{m^{2}} \left(l^{2} + 2 + \frac{1}{l^{2}}\right) - \frac{1}{l^{2}}) |
lidless mm-cpn in the closed state with atp/alfx |
 |
 |
=2 l^{6} + 7 l^{4} + 8 l^{2} + m^{4} \left(l^{4} + l^{2}\right) + m^{2} \left(- l^{6} - 5 l^{4} - 5 l^{2} - 1\right) + 3 + \frac{1}{m^{2}} \left(- l^{6} - 4 l^{4} - 5 l^{2} - 2\right)) |
crystal structure of e. coli nadp dependent enzyme |
 |
 |
=m^{4} \left(\frac{1}{l^{2}} + \frac{1}{l^{4}}\right) + m^{2} \left(-1 - \frac{5}{l^{2}} - \frac{5}{l^{4}} - \frac{1}{l^{6}}\right) + 3 + \frac{1}{m^{2}} \left(-2 - \frac{5}{l^{2}} - \frac{4}{l^{4}} - \frac{1}{l^{6}}\right) + \frac{8}{l^{2}} + \frac{7}{l^{4}} + \frac{2}{l^{6}}) |
human class i mhc hla-a2(a150p) in complex with the tax peptide |
 |
 |
=m^{2} \left(\frac{1}{l^{2}} - \frac{1}{l^{4}} - \frac{2}{l^{6}}\right) + \frac{1}{m^{2}} \left(- \frac{2}{l^{4}} - \frac{5}{l^{6}} - \frac{4}{l^{8}} - \frac{1}{l^{10}}\right) - \frac{1}{l^{2}} + \frac{3}{l^{4}} + \frac{7}{l^{6}} + \frac{3}{l^{8}}) |
lidless mm-cpn in the closed state with atp/alfx |
 |
 |
=2 l^{4} + 8 l^{2} + m^{4} \left(l^{2} + 1\right) + m^{2} \left(- l^{4} - 5 l^{2} - 5 - \frac{1}{l^{2}}\right) + 8 + \frac{1}{m^{2}} \left(- 2 l^{4} - 5 l^{2} - 4 - \frac{1}{l^{2}}\right) + \frac{2}{l^{2}}) |
crystal structure of e. coli nadp dependent enzyme |
 |
 |
=3 l^{8} + 7 l^{6} + 3 l^{4} - l^{2} + m^{2} \left(- 2 l^{6} - l^{4} + l^{2}\right) + \frac{1}{m^{2}} \left(- l^{10} - 4 l^{8} - 5 l^{6} - 2 l^{4}\right)) |
crystal structure of archaeal 20s proteasome in complex with 2 mutated p26 activator |
 |
 |
=2 l^{2} + m^{4} \left(1 + \frac{1}{l^{2}}\right) + m^{2} \left(- l^{2} - 5 - \frac{5}{l^{2}} - \frac{1}{l^{4}}\right) + 8 + \frac{1}{m^{2}} \left(- l^{2} - 4 - \frac{5}{l^{2}} - \frac{2}{l^{4}}\right) + \frac{8}{l^{2}} + \frac{2}{l^{4}}) |
crystal structure of e. coli nadp dependent enzyme |
 |
 |
=l^{2} + m^{4} \left(1 + \frac{1}{l^{2}}\right) + m^{2} \left(- l^{2} - 4 - \frac{4}{l^{2}} - \frac{1}{l^{4}}\right) + 3 + \frac{1}{m^{2}} \left(l^{2} + 2 + \frac{1}{l^{2}}\right) + \frac{3}{l^{2}} + \frac{1}{l^{4}}) |
crystal structure of archaeal 20s proteasome in complex with 2 mutated p26 activator |
 |
 |
=l^{4} + 3 l^{2} + m^{4} \left(l^{2} + 1\right) + m^{2} \left(- l^{4} - 4 l^{2} - 4 - \frac{1}{l^{2}}\right) + 3 + \frac{1}{m^{2}} \left(l^{2} + 2 + \frac{1}{l^{2}}\right) + \frac{1}{l^{2}}) |
human class i mhc hla-a2(a150p) in complex with the tax peptide |
 |
 |
=4 l^{8} + 10 l^{6} + 6 l^{4} + m^{4} \left(l^{6} + l^{4}\right) + m^{2} \left(- l^{8} - 6 l^{6} - 5 l^{4}\right) + \frac{1}{m^{2}} \left(- l^{10} - 4 l^{8} - 5 l^{6} - 2 l^{4}\right)) |
cystal structure of rhesus macaque mhc class i:mamu-a*02 |
 |
 |
=l^{2} + m^{2} \left(-1 - \frac{1}{l^{2}}\right) + 5 + \frac{1}{m^{2}} \left(- l^{2} - 4 - \frac{5}{l^{2}} - \frac{2}{l^{4}}\right) + \frac{5}{l^{2}} + \frac{1}{l^{4}}) |
crystal structure of e. coli nadp dependent enzyme |
 |
 |
=m^{4} \left(\frac{1}{l^{4}} + \frac{1}{l^{6}}\right) + m^{2} \left(- \frac{5}{l^{4}} - \frac{6}{l^{6}} - \frac{1}{l^{8}}\right) + \frac{1}{m^{2}} \left(- \frac{2}{l^{4}} - \frac{5}{l^{6}} - \frac{4}{l^{8}} - \frac{1}{l^{10}}\right) + \frac{6}{l^{4}} + \frac{10}{l^{6}} + \frac{4}{l^{8}}) |
cystal structure of rhesus macaque mhc class i:mamu-a*02 |
 |
 |
=l^{4} + 5 l^{2} + m^{2} \left(- l^{2} - 1\right) + 5 + \frac{1}{m^{2}} \left(- 2 l^{4} - 5 l^{2} - 4 - \frac{1}{l^{2}}\right) + \frac{1}{l^{2}}) |
copper amine oxidase from hansenula polymorpha |
 |
 |
=l^{4} + 3 l^{2} + m^{4} + m^{2} \left(- 2 l^{2} - 2 - \frac{1}{l^{2}}\right) + 2 + \frac{1}{m^{2}} \left(- l^{4} - 2 l^{2} - 1\right)) |
refinement of the influenza virus hemagglutinin by simulated annealing |
 |
 |
=m^{4} \left(\frac{1}{l^{4}} - \frac{1}{l^{6}}\right) + m^{2} \left(- \frac{3}{l^{4}} + \frac{1}{l^{6}} + \frac{1}{l^{8}}\right) + \frac{1}{m^{2}} \left(- \frac{1}{l^{4}} - \frac{2}{l^{6}} - \frac{1}{l^{8}}\right) + \frac{3}{l^{4}} + \frac{3}{l^{6}}) |
crystal structure of e. coli nadp dependent enzyme |
 |
 |
=m^{4} + m^{2} \left(- l^{2} - 2 - \frac{2}{l^{2}}\right) + 2 + \frac{1}{m^{2}} \left(-1 - \frac{2}{l^{2}} - \frac{1}{l^{4}}\right) + \frac{3}{l^{2}} + \frac{1}{l^{4}}) |
cystal structure of rhesus macaque mhc class i:mamu-a*02 |
 |
 |
=3 l^{6} + 3 l^{4} + m^{4} \left(- l^{6} + l^{4}\right) + m^{2} \left(l^{8} + l^{6} - 3 l^{4}\right) + \frac{1}{m^{2}} \left(- l^{8} - 2 l^{6} - l^{4}\right)) |
poliovirus late rna-release intermediate |
 |
 |
=l^{4} + 5 l^{2} + m^{4} \left(l^{2} + 1\right) + m^{2} \left(- l^{4} - 4 l^{2} - 5 - \frac{2}{l^{2}}\right) + 8 + \frac{1}{m^{2}} \left(- l^{4} - 3 l^{2} - 4 - \frac{3}{l^{2}} - \frac{1}{l^{4}}\right) + \frac{5}{l^{2}} + \frac{1}{l^{4}}) |
hiv protease, pseudo-symmetric inhibitors |
 |
 |
=- l^{10} + l^{8} + 7 l^{6} + 5 l^{4} + m^{4} \left(- l^{8} + l^{4}\right) + m^{2} \left(l^{10} + 3 l^{8} - 2 l^{6} - 4 l^{4}\right) + \frac{1}{m^{2}} \left(- l^{10} - 4 l^{8} - 5 l^{6} - 2 l^{4}\right)) |
crystal structure of tyrosine aminotransferase tripple mutant (p181q, 2 r183g,a321k) from escherichia coli at 2.35 a resolution |
 |
 |
=l^{4} + 4 l^{2} + m^{4} \left(l^{2} + 1\right) + m^{2} \left(- l^{4} - 4 l^{2} - 5 - \frac{2}{l^{2}}\right) + 8 + \frac{1}{m^{2}} \left(- l^{2} - 4 - \frac{5}{l^{2}} - \frac{2}{l^{4}}\right) + \frac{6}{l^{2}} + \frac{1}{l^{4}}) |
crystal structure of tyrosine aminotransferase tripple mutant (p181q, 2 r183g,a321k) from escherichia coli at 2.35 a resolution |
 |
 |
=l^{4} + 6 l^{2} + m^{4} \left(1 + \frac{1}{l^{2}}\right) + m^{2} \left(- 2 l^{2} - 5 - \frac{4}{l^{2}} - \frac{1}{l^{4}}\right) + 8 + \frac{1}{m^{2}} \left(- 2 l^{4} - 5 l^{2} - 4 - \frac{1}{l^{2}}\right) + \frac{4}{l^{2}} + \frac{1}{l^{4}}) |
crystal structure of e. coli nadp dependent enzyme |
 |
 |
=- l^{8} + 1 + \frac{1}{m^{2}} \left(l^{10} + 2 l^{8} + l^{6}\right)) |
ribonuclease inhibitor-angiogenin complex |
 |
 |
=l^{2} + m^{4} \left(1 + \frac{1}{l^{2}}\right) + m^{2} \left(- l^{2} - 4 - \frac{5}{l^{2}} - \frac{2}{l^{4}}\right) + 5 + \frac{1}{m^{2}} \left(-2 - \frac{5}{l^{2}} - \frac{4}{l^{4}} - \frac{1}{l^{6}}\right) + \frac{8}{l^{2}} + \frac{5}{l^{4}} + \frac{1}{l^{6}}) |
crystal structure of archaeal 20s proteasome in complex with 2 mutated p26 activator |
 |
 |
=l^{2} + m^{4} \left(1 + \frac{1}{l^{2}}\right) + m^{2} \left(- l^{2} - 4 - \frac{5}{l^{2}} - \frac{2}{l^{4}}\right) + 5 + \frac{1}{m^{2}} \left(-2 - \frac{5}{l^{2}} - \frac{4}{l^{4}} - \frac{1}{l^{6}}\right) + \frac{8}{l^{2}} + \frac{5}{l^{4}} + \frac{1}{l^{6}}) |
crystal structure of e. coli nadp dependent enzyme |
 |
 |
=m^{6} \left(\frac{1}{l^{6}} + \frac{1}{l^{8}}\right) + m^{4} \left(- \frac{7}{l^{6}} - \frac{8}{l^{8}} - \frac{1}{l^{10}}\right) + m^{2} \left(\frac{15}{l^{6}} + \frac{20}{l^{8}} + \frac{5}{l^{10}}\right) + \frac{1}{m^{2}} \left(\frac{1}{l^{6}} + \frac{2}{l^{8}} + \frac{1}{l^{10}}\right) - \frac{10}{l^{6}} - \frac{16}{l^{8}} - \frac{6}{l^{10}}) |
hiv gp41 six-helix bundle containing a mutant chr alpha- 2 peptide sequence |
 |
 |
=1 + \frac{1}{m^{2}} \left(\frac{1}{l^{6}} + \frac{2}{l^{8}} + \frac{1}{l^{10}}\right) - \frac{1}{l^{8}}) |
crystal structure of adenylylsulfate reductase from 2 desulfovibrio gigas |
 |
 |
=- 6 l^{10} - 16 l^{8} - 10 l^{6} + m^{6} \left(l^{8} + l^{6}\right) + m^{4} \left(- l^{10} - 8 l^{8} - 7 l^{6}\right) + m^{2} \left(5 l^{10} + 20 l^{8} + 15 l^{6}\right) + \frac{1}{m^{2}} \left(l^{10} + 2 l^{8} + l^{6}\right)) |
rabbit muscle l-lactate dehydrogenase in complex with nadh and oxamate |
 |
 |
=2 l^{2} + m^{2} \left(-1 - \frac{1}{l^{2}}\right) + 5 + \frac{1}{m^{2}} \left(- l^{4} - 3 l^{2} - 4 - \frac{3}{l^{2}} - \frac{1}{l^{4}}\right) + \frac{4}{l^{2}} + \frac{1}{l^{4}}) |
crystal structure of e. coli nadp dependent enzyme |
 |
 |
=l^{4} + 4 l^{2} + m^{2} \left(- l^{2} - 1\right) + 5 + \frac{1}{m^{2}} \left(- l^{4} - 3 l^{2} - 4 - \frac{3}{l^{2}} - \frac{1}{l^{4}}\right) + \frac{2}{l^{2}}) |
crystal structure of e. coli nadp dependent enzyme |
 |
 |
=3 l^{6} + 7 l^{4} + 7 l^{2} + m^{4} \left(l^{4} + l^{2}\right) + m^{2} \left(- l^{6} - 5 l^{4} - 5 l^{2} - 1\right) + 3 + \frac{1}{m^{2}} \left(- l^{8} - 3 l^{6} - 4 l^{4} - 3 l^{2} - 1\right)) |
lidless mm-cpn in the closed state with atp/alfx |
 |
 |
=m^{2} \left(- \frac{1}{l^{2}} - \frac{1}{l^{4}}\right) + 2 + \frac{1}{m^{2}} \left(-1 - \frac{3}{l^{2}} - \frac{4}{l^{4}} - \frac{3}{l^{6}} - \frac{1}{l^{8}}\right) + \frac{4}{l^{2}} + \frac{4}{l^{4}} + \frac{2}{l^{6}}) |
rational development of high-affinity t-cell receptor-like antibodies |
 |
 |
=m^{4} \left(\frac{1}{l^{2}} + \frac{1}{l^{4}}\right) + m^{2} \left(-1 - \frac{5}{l^{2}} - \frac{5}{l^{4}} - \frac{1}{l^{6}}\right) + 3 + \frac{1}{m^{2}} \left(-1 - \frac{3}{l^{2}} - \frac{4}{l^{4}} - \frac{3}{l^{6}} - \frac{1}{l^{8}}\right) + \frac{7}{l^{2}} + \frac{7}{l^{4}} + \frac{3}{l^{6}}) |
crystal structure of e. coli nadp dependent enzyme |
 |
 |
=2 l^{6} + 4 l^{4} + 4 l^{2} + m^{2} \left(- l^{4} - l^{2}\right) + 2 + \frac{1}{m^{2}} \left(- l^{8} - 3 l^{6} - 4 l^{4} - 3 l^{2} - 1\right)) |
poliovirus late rna-release intermediate |
 |
 |
=- 3 l^{10} - 7 l^{8} - l^{6} + 3 l^{4} + m^{4} \left(- l^{8} + l^{4}\right) + m^{2} \left(l^{10} + 5 l^{8} - 4 l^{4}\right) + \frac{1}{m^{2}} \left(l^{10} + 2 l^{8} + l^{6}\right)) |
crystal structure of the sodium-potassium pump |
 |
 |
=m^{2} \left(\frac{1}{l^{2}} + \frac{1}{l^{8}}\right) + \frac{1}{m^{2}} \left(\frac{1}{l^{6}} + \frac{2}{l^{8}} + \frac{1}{l^{10}}\right) - \frac{2}{l^{2}} - \frac{1}{l^{4}} - \frac{1}{l^{6}} - \frac{3}{l^{8}} - \frac{1}{l^{10}}) |
crystal structure of adenylylsulfate reductase from 2 desulfovibrio gigas |
 |
 |
=m^{4} \left(\frac{1}{l^{4}} - \frac{1}{l^{8}}\right) + m^{2} \left(- \frac{4}{l^{4}} + \frac{5}{l^{8}} + \frac{1}{l^{10}}\right) + \frac{1}{m^{2}} \left(\frac{1}{l^{6}} + \frac{2}{l^{8}} + \frac{1}{l^{10}}\right) + \frac{3}{l^{4}} - \frac{1}{l^{6}} - \frac{7}{l^{8}} - \frac{3}{l^{10}}) |
refinement of the influenza virus hemagglutinin by simulated annealing |
 |
 |
=- l^{10} - 3 l^{8} - l^{6} - l^{4} - 2 l^{2} + m^{2} \left(l^{8} + l^{2}\right) + \frac{1}{m^{2}} \left(l^{10} + 2 l^{8} + l^{6}\right)) |
lidless mm-cpn in the closed state with atp/alfx |
 |
 |
=m^{4} \left(\frac{1}{l^{4}} - \frac{1}{l^{8}}\right) + m^{2} \left(- \frac{4}{l^{4}} - \frac{1}{l^{6}} + \frac{4}{l^{8}} + \frac{1}{l^{10}}\right) + \frac{1}{m^{2}} \left(- \frac{1}{l^{4}} - \frac{2}{l^{6}} - \frac{1}{l^{8}}\right) + \frac{4}{l^{4}} + \frac{3}{l^{6}} - \frac{3}{l^{8}} - \frac{2}{l^{10}}) |
crystal structure of the sodium-potassium pump |
 |
 |
=2 l^{6} + 2 l^{4} + m^{2} \left(- l^{4} + 1\right) - 1 + \frac{1}{m^{2}} \left(- l^{8} - 2 l^{6} - l^{4}\right) - \frac{1}{l^{2}}) |
lidless mm-cpn in the closed state with atp/alfx |
 |
 |
=- 2 l^{10} - 3 l^{8} + 3 l^{6} + 4 l^{4} + m^{4} \left(- l^{8} + l^{4}\right) + m^{2} \left(l^{10} + 4 l^{8} - l^{6} - 4 l^{4}\right) + \frac{1}{m^{2}} \left(- l^{8} - 2 l^{6} - l^{4}\right)) |
crystal structure of archaeal 20s proteasome in complex with 2 mutated p26 activator |
 |
 |
=- l^{2} + m^{2} \left(1 - \frac{1}{l^{4}}\right) - 1 + \frac{1}{m^{2}} \left(- \frac{1}{l^{4}} - \frac{2}{l^{6}} - \frac{1}{l^{8}}\right) + \frac{2}{l^{4}} + \frac{2}{l^{6}}) |
lidless mm-cpn in the closed state with atp/alfx |
 |
 |
=m^{2} \left(\frac{1}{l^{2}} - \frac{1}{l^{4}} - \frac{1}{l^{6}} + \frac{1}{l^{8}}\right) + \frac{1}{m^{2}} \left(\frac{1}{l^{6}} + \frac{2}{l^{8}} + \frac{1}{l^{10}}\right) - \frac{1}{l^{2}} + \frac{2}{l^{4}} + \frac{2}{l^{6}} - \frac{2}{l^{8}} - \frac{1}{l^{10}}) |
copper amine oxidase from hansenula polymorpha |
 |
 |
=- 2 l^{10} - 4 l^{8} + 2 l^{6} + 4 l^{4} + m^{4} \left(- l^{8} + l^{4}\right) + m^{2} \left(l^{10} + 4 l^{8} - l^{6} - 4 l^{4}\right) + \frac{1}{m^{2}} \left(l^{10} + 2 l^{8} + l^{6}\right)) |
lidless mm-cpn in the closed state with atp/alfx |
 |
 |
=m^{2} \left(\frac{1}{l^{2}} - \frac{1}{l^{4}} - \frac{1}{l^{6}} + \frac{1}{l^{8}}\right) + \frac{1}{m^{2}} \left(- \frac{1}{l^{4}} - \frac{2}{l^{6}} - \frac{1}{l^{8}}\right) - \frac{1}{l^{2}} + \frac{2}{l^{4}} + \frac{3}{l^{6}} - \frac{1}{l^{8}} - \frac{1}{l^{10}}) |
crystal structure of the sodium-potassium pump |
 |
 |
=l^{8} + 5 l^{6} + 6 l^{4} + 4 l^{2} + m^{4} \left(l^{4} + l^{2}\right) + m^{2} \left(- 2 l^{6} - 5 l^{4} - 4 l^{2} - 1\right) + 2 + \frac{1}{m^{2}} \left(- l^{8} - 2 l^{6} - l^{4}\right)) |
crystal structure of e. coli nadp dependent enzyme |
 |
 |
=- l^{10} - l^{8} + 3 l^{6} + 2 l^{4} - l^{2} + m^{2} \left(l^{8} - l^{6} - l^{4} + l^{2}\right) + \frac{1}{m^{2}} \left(- l^{8} - 2 l^{6} - l^{4}\right)) |
lidless mm-cpn in the closed state with atp/alfx |
 |
 |
=m^{4} \left(\frac{1}{l^{2}} + \frac{1}{l^{4}}\right) + m^{2} \left(-1 - \frac{4}{l^{2}} - \frac{5}{l^{4}} - \frac{2}{l^{6}}\right) + 2 + \frac{1}{m^{2}} \left(- \frac{1}{l^{4}} - \frac{2}{l^{6}} - \frac{1}{l^{8}}\right) + \frac{4}{l^{2}} + \frac{6}{l^{4}} + \frac{5}{l^{6}} + \frac{1}{l^{8}}) |
crystal structure of adenylylsulfate reductase from 2 desulfovibrio gigas |
 |
 |
=m^{2} \left(\frac{1}{l^{2}} + \frac{1}{l^{8}}\right) + \frac{1}{m^{2}} \left(\frac{1}{l^{2}} + \frac{2}{l^{4}} + \frac{1}{l^{6}}\right) - \frac{2}{l^{2}} - \frac{2}{l^{4}} - \frac{1}{l^{6}} - \frac{2}{l^{8}} - \frac{1}{l^{10}}) |
refinement of the influenza virus hemagglutinin by simulated annealing |
 |
 |
=- 2 l^{4} - 2 l^{2} + m^{2} \left(l^{2} - \frac{1}{l^{2}}\right) + 1 + \frac{1}{m^{2}} \left(l^{6} + 2 l^{4} + l^{2}\right) + \frac{2}{l^{2}} + \frac{1}{l^{4}}) |
lidless mm-cpn in the closed state with atp/alfx |
 |
 |
=- l^{10} - 2 l^{8} - l^{6} - 2 l^{4} - 2 l^{2} + m^{2} \left(l^{8} + l^{2}\right) + \frac{1}{m^{2}} \left(l^{6} + 2 l^{4} + l^{2}\right)) |
crystal structure of blub-like flavoprotein (yp_001089088.1) from 2 clostridium difficile 630 at 1.74 a resolution |
 |
 |
=l^{4} + 2 l^{2} + m^{2} \left(- l^{2} + \frac{1}{l^{2}}\right) + 1 + \frac{1}{m^{2}} \left(\frac{1}{l^{2}} + \frac{2}{l^{4}} + \frac{1}{l^{6}}\right) - \frac{2}{l^{2}} - \frac{2}{l^{4}}) |
refinement of the influenza virus hemagglutinin by simulated annealing |
 |
 |
=l^{4} + 5 l^{2} + m^{4} \left(1 + \frac{1}{l^{2}}\right) + m^{2} \left(- 2 l^{2} - 5 - \frac{4}{l^{2}} - \frac{1}{l^{4}}\right) + 7 + \frac{1}{m^{2}} \left(- l^{4} - 2 l^{2} - 1\right) + \frac{4}{l^{2}} + \frac{1}{l^{4}}) |
crystal structure of adenylylsulfate reductase from 2 desulfovibrio gigas |
 |
 |
=m^{4} \left(\frac{1}{l^{2}} + \frac{1}{l^{4}}\right) + m^{2} \left(-1 - \frac{4}{l^{2}} - \frac{5}{l^{4}} - \frac{2}{l^{6}}\right) + 2 + \frac{1}{m^{2}} \left(-1 - \frac{2}{l^{2}} - \frac{1}{l^{4}}\right) + \frac{5}{l^{2}} + \frac{6}{l^{4}} + \frac{4}{l^{6}} + \frac{1}{l^{8}}) |
crystal structure of e. coli nadp dependent enzyme |
 |
 |
=l^{4} + 4 l^{2} + m^{4} \left(l^{2} + 1\right) + m^{2} \left(- l^{4} - 4 l^{2} - 5 - \frac{2}{l^{2}}\right) + 7 + \frac{1}{m^{2}} \left(-1 - \frac{2}{l^{2}} - \frac{1}{l^{4}}\right) + \frac{5}{l^{2}} + \frac{1}{l^{4}}) |
poliovirus early rna-release intermediate |
 |
 |
=l^{8} + 4 l^{6} + 6 l^{4} + 5 l^{2} + m^{4} \left(l^{4} + l^{2}\right) + m^{2} \left(- 2 l^{6} - 5 l^{4} - 4 l^{2} - 1\right) + 2 + \frac{1}{m^{2}} \left(- l^{4} - 2 l^{2} - 1\right)) |
crystal structure of adenylylsulfate reductase from 2 desulfovibrio gigas |
 |
 |
=l^{2} + m^{4} \left(1 + \frac{1}{l^{2}}\right) + m^{2} \left(- l^{2} - 4 - \frac{5}{l^{2}} - \frac{2}{l^{4}}\right) + 5 + \frac{1}{m^{2}} \left(-1 - \frac{2}{l^{2}} - \frac{1}{l^{4}}\right) + \frac{7}{l^{2}} + \frac{4}{l^{4}} + \frac{1}{l^{6}}) |
copper amine oxidase from hansenula polymorpha |
 |
 |
=l^{6} + 4 l^{4} + 7 l^{2} + m^{4} \left(l^{2} + 1\right) + m^{2} \left(- 2 l^{4} - 5 l^{2} - 4 - \frac{1}{l^{2}}\right) + 5 + \frac{1}{m^{2}} \left(- l^{4} - 2 l^{2} - 1\right) + \frac{1}{l^{2}}) |
rational development of high-affinity t-cell receptor-like antibodies |
 |
 |
=l^{8} + 5 l^{6} + 7 l^{4} + 5 l^{2} + m^{4} \left(l^{4} + l^{2}\right) + m^{2} \left(- 2 l^{6} - 5 l^{4} - 4 l^{2} - 1\right) + 2 + \frac{1}{m^{2}} \left(- l^{8} - 3 l^{6} - 4 l^{4} - 3 l^{2} - 1\right)) |
structure of glutamate dehydrogenase complexed with 2 bithionol |
 |
 |
=- l^{2} + m^{2} \left(1 - \frac{1}{l^{2}} - \frac{2}{l^{4}}\right) + \frac{1}{m^{2}} \left(-1 - \frac{3}{l^{2}} - \frac{4}{l^{4}} - \frac{3}{l^{6}} - \frac{1}{l^{8}}\right) + \frac{4}{l^{2}} + \frac{6}{l^{4}} + \frac{3}{l^{6}}) |
refinement of the influenza virus hemagglutinin by simulated annealing |
 |
 |
=m^{4} \left(\frac{1}{l^{2}} + \frac{1}{l^{4}}\right) + m^{2} \left(-1 - \frac{4}{l^{2}} - \frac{5}{l^{4}} - \frac{2}{l^{6}}\right) + 2 + \frac{1}{m^{2}} \left(-1 - \frac{3}{l^{2}} - \frac{4}{l^{4}} - \frac{3}{l^{6}} - \frac{1}{l^{8}}\right) + \frac{5}{l^{2}} + \frac{7}{l^{4}} + \frac{5}{l^{6}} + \frac{1}{l^{8}}) |
copper amine oxidase from hansenula polymorpha |
 |
 |
=3 l^{6} + 6 l^{4} + 4 l^{2} + m^{2} \left(- 2 l^{4} - l^{2} + 1\right) + \frac{1}{m^{2}} \left(- l^{8} - 3 l^{6} - 4 l^{4} - 3 l^{2} - 1\right) - \frac{1}{l^{2}}) |
crystal structure of adenylylsulfate reductase from 2 desulfovibrio gigas |
 |
 |
=- 2 l^{8} + l^{4} m^{4} - 4 l^{4} m^{2} + 2 l^{4} + \frac{1}{m^{2}} \left(l^{10} + 2 l^{8} + l^{6}\right)) |
crystal structure of adenylylsulfate reductase from 2 desulfovibrio gigas |
 |
 |
=- 3 l^{2} - m^{4} + m^{2} \left(l^{2} + 5\right) - 5 + \frac{1}{m^{2}} \left(l^{2} + 2 + \frac{1}{l^{2}}\right) - \frac{1}{l^{2}} + \frac{1}{l^{4}}) |
refinement of the influenza virus hemagglutinin by simulated annealing |
 |
 |
=- 2 l^{8} + l^{4} m^{4} - 4 l^{4} m^{2} + 2 l^{4} + \frac{1}{m^{2}} \left(l^{10} + 2 l^{8} + l^{6}\right)) |
refinement of the influenza virus hemagglutinin by simulated annealing |
 |
 |
=m^{5} \left(- l^{5} - l^{3}\right) + m^{3} \left(l^{7} + 6 l^{5} + 6 l^{3} + l\right) + m \left(- 3 l^{7} - 11 l^{5} - 12 l^{3} - 4 l\right) + \frac{1}{m} \left(2 l^{7} + 8 l^{5} + 10 l^{3} + 4 l\right) + \frac{1}{m^{3}} \left(- l^{7} - 3 l^{5} - 3 l^{3} - l\right)) |
cystal structure of rhesus macaque mhc class i:mamu-a*02 |
 |
 |
=m^{2} \left(\frac{1}{l^{2}} - \frac{2}{l^{4}} + \frac{2}{l^{6}}\right) + \frac{1}{m^{2}} \left(\frac{1}{l^{6}} + \frac{2}{l^{8}} + \frac{1}{l^{10}}\right) + \frac{1}{l^{4}} - \frac{2}{l^{6}} - \frac{3}{l^{8}}) |
refinement of the influenza virus hemagglutinin by simulated annealing |
 |
 |
=- 2 l^{6} + l^{4} m^{6} - 6 l^{4} - 4 l^{2} + m^{4} \left(- l^{6} - 5 l^{4} - l^{2}\right) + m^{2} \left(3 l^{6} + 8 l^{4} + 4 l^{2}\right) + \frac{1}{m^{2}} \left(l^{6} + 2 l^{4} + l^{2}\right)) |
coiled-coil domain of tumor susceptibility gene 101 |
 |
 |
=m^{2} \left(\frac{1}{l^{2}} - \frac{2}{l^{4}} + \frac{2}{l^{6}}\right) + \frac{1}{m^{2}} \left(\frac{1}{l^{6}} + \frac{2}{l^{8}} + \frac{1}{l^{10}}\right) + \frac{1}{l^{4}} - \frac{2}{l^{6}} - \frac{3}{l^{8}}) |
crystal structure of e. coli nadp dependent enzyme |
 |
 |
=- l^{6} - 3 l^{4} - l^{2} + m^{4} \left(- l^{4} + l^{2}\right) + m^{2} \left(l^{6} + 2 l^{4} - l^{2} - 1\right) + 1 + \frac{1}{m^{2}} \left(l^{6} + 2 l^{4} + l^{2}\right)) |
crystal structure of e. coli nadp dependent enzyme |
 |
 |
=- 3 l^{2} + m^{6} + m^{4} \left(- l^{2} - 5 - \frac{1}{l^{2}}\right) + m^{2} \left(3 l^{2} + 9 + \frac{3}{l^{2}}\right) - 6 + \frac{1}{m^{2}} \left(l^{2} + 2 + \frac{1}{l^{2}}\right) - \frac{3}{l^{2}}) |
crystal structure of e. coli nadp dependent enzyme |
 |
 |
=- l^{6} - 3 l^{4} - l^{2} + m^{4} \left(- l^{4} + l^{2}\right) + m^{2} \left(l^{6} + 2 l^{4} - l^{2} - 1\right) + 1 + \frac{1}{m^{2}} \left(l^{6} + 2 l^{4} + l^{2}\right)) |
cystal structure of rhesus macaque mhc class i:mamu-a*02 |
 |
 |
=m^{2} \left(-1 - \frac{1}{l^{2}} - \frac{3}{l^{4}}\right) + \frac{1}{m^{2}} \left(- \frac{1}{l^{4}} - \frac{2}{l^{6}} - \frac{1}{l^{8}}\right) + \frac{m^{4}}{l^{2}} + \frac{3}{l^{4}} + \frac{3}{l^{6}}) |
refinement of the influenza virus hemagglutinin by simulated annealing |
 |
 |
=l^{4} + 3 l^{2} + m^{4} \left(- l^{4} + l^{2}\right) + m^{2} \left(l^{6} + l^{4} - 2 l^{2} - 1\right) + 2 + \frac{1}{m^{2}} \left(- l^{4} - 2 l^{2} - 1\right)) |
poliovirus early rna-release intermediate |
 |
 |
=l^{4} + 3 l^{2} + m^{4} \left(- l^{4} + l^{2}\right) + m^{2} \left(l^{6} + l^{4} - 2 l^{2} - 1\right) + 2 + \frac{1}{m^{2}} \left(- l^{4} - 2 l^{2} - 1\right)) |
crystal structure of e. coli nadp dependent enzyme |
 |
 |
=l^{4} + 3 l^{2} + m^{4} \left(- l^{4} + l^{2}\right) + m^{2} \left(l^{6} + l^{4} - 2 l^{2} - 1\right) + 2 + \frac{1}{m^{2}} \left(- l^{4} - 2 l^{2} - 1\right)) |
crystal structure of the sodium-potassium pump |
 |
 |
=m^{4} \left(\frac{1}{l^{4}} - \frac{2}{l^{6}}\right) + m^{2} \left(- \frac{2}{l^{4}} + \frac{5}{l^{6}} + \frac{3}{l^{8}}\right) + \frac{1}{m^{2}} \left(\frac{1}{l^{6}} + \frac{2}{l^{8}} + \frac{1}{l^{10}}\right) + \frac{1}{l^{4}} - \frac{3}{l^{6}} - \frac{5}{l^{8}} - \frac{1}{l^{10}}) |
rational development of high-affinity t-cell receptor-like antibodies |
 |
 |
=- l^{10} - 5 l^{8} - 3 l^{6} + l^{4} + m^{4} \left(- 2 l^{6} + l^{4}\right) + m^{2} \left(3 l^{8} + 5 l^{6} - 2 l^{4}\right) + \frac{1}{m^{2}} \left(l^{10} + 2 l^{8} + l^{6}\right)) |
crystal structure of adenylylsulfate reductase from 2 desulfovibrio gigas |
 |
 |
=m^{4} \left(-1 - \frac{4}{l^{2}} - \frac{1}{l^{4}}\right) + m^{2} \left(2 + \frac{4}{l^{2}} + \frac{2}{l^{4}}\right) + 1 + \frac{1}{m^{2}} \left(-1 - \frac{2}{l^{2}} - \frac{1}{l^{4}}\right) + \frac{m^{6}}{l^{2}} + \frac{1}{l^{2}}) |
crystal structure of the nadp-dependent mannitol dehydrogenase from 2 cladosporium herbarum. |
 |
 |
=l^{2} + m^{4} \left(- l^{2} + 1\right) + m^{2} \left(l^{4} + l^{2} - 1 - \frac{1}{l^{2}}\right) + 1 + \frac{1}{m^{2}} \left(- l^{4} - 2 l^{2} - 1\right)) |
crystal structure of e. coli nadp dependent enzyme |
 |
 |
=l^{2} + m^{4} \left(- l^{2} + 1\right) + m^{2} \left(l^{4} + l^{2} - 1 - \frac{1}{l^{2}}\right) + 1 + \frac{1}{m^{2}} \left(- l^{4} - 2 l^{2} - 1\right)) |
rational development of high-affinity t-cell receptor-like antibodies |
 |
 |
=- l^{2} + m^{6} + m^{4} \left(- l^{2} - 4 - \frac{1}{l^{2}}\right) + m^{2} \left(2 l^{2} + 5 + \frac{2}{l^{2}}\right) - 2 + \frac{1}{m^{2}} \left(l^{2} + 2 + \frac{1}{l^{2}}\right) - \frac{1}{l^{2}}) |
crystal structure of adenylylsulfate reductase from 2 desulfovibrio gigas |
 |
 |
=- 2 l^{4} - 2 l^{2} + m^{4} \left(- l^{4} + l^{2}\right) + m^{2} \left(l^{6} + l^{4} - 1\right) + \frac{1}{m^{2}} \left(l^{6} + 2 l^{4} + l^{2}\right)) |
human class i mhc hla-a2(a150p) in complex with the tel1p peptide |
 |
 |
=- l^{2} + m^{6} + m^{4} \left(- l^{2} - 4 - \frac{1}{l^{2}}\right) + m^{2} \left(2 l^{2} + 5 + \frac{2}{l^{2}}\right) - 2 + \frac{1}{m^{2}} \left(l^{2} + 2 + \frac{1}{l^{2}}\right) - \frac{1}{l^{2}}) |
complex of fimc, fimf, fimg and fimh |
 |
 |
=1 + \frac{1}{m^{2}} \left(\frac{1}{l^{2}} + \frac{2}{l^{4}} + \frac{1}{l^{6}}\right) - \frac{1}{l^{2}} + \frac{m^{2}}{l^{4}} - \frac{3}{l^{4}} - \frac{1}{l^{6}}) |
refinement of the influenza virus hemagglutinin by simulated annealing |
 |
 |
=- 3 l^{2} - m^{4} + m^{2} \left(l^{2} + 5 + \frac{1}{l^{2}}\right) - 6 + \frac{1}{m^{2}} \left(l^{2} + 2 + \frac{1}{l^{2}}\right) - \frac{3}{l^{2}}) |
crystal structure of human apolipoprotein a-i |
 |
 |
=1 + \frac{1}{m^{2}} \left(\frac{1}{l^{2}} + \frac{2}{l^{4}} + \frac{1}{l^{6}}\right) - \frac{1}{l^{2}} + \frac{m^{2}}{l^{4}} - \frac{3}{l^{4}} - \frac{1}{l^{6}}) |
crystal structure of human apolipoprotein a-i |
 |
 |
=- 3 l^{8} - 2 l^{6} + l^{4} + m^{4} \left(- l^{6} + l^{4}\right) + m^{2} \left(l^{8} + 3 l^{6} - 3 l^{4}\right) + \frac{1}{m^{2}} \left(l^{10} + 2 l^{8} + l^{6}\right)) |
crystal structure of e. coli nadp dependent enzyme |
 |
 |
=m^{2} \left(\frac{2}{l^{2}} + \frac{4}{l^{4}} + \frac{1}{l^{6}}\right) + \frac{1}{m^{2}} \left(\frac{1}{l^{2}} + \frac{2}{l^{4}} + \frac{1}{l^{6}}\right) - \frac{4}{l^{2}} - \frac{m^{4}}{l^{4}} - \frac{6}{l^{4}} - \frac{2}{l^{6}}) |
coiled-coil domain of tumor susceptibility gene 101 |
 |
 |
=- 2 l^{2} + m^{2} \left(2 - \frac{1}{l^{2}}\right) - 3 + \frac{1}{m^{2}} \left(l^{2} + 2 + \frac{1}{l^{2}}\right) + \frac{1}{l^{4}}) |
crystal structure of e. coli nadp dependent enzyme |
 |
 |
=m^{2} \left(\frac{2}{l^{2}} + \frac{4}{l^{4}} + \frac{1}{l^{6}}\right) + \frac{1}{m^{2}} \left(\frac{1}{l^{2}} + \frac{2}{l^{4}} + \frac{1}{l^{6}}\right) - \frac{4}{l^{2}} - \frac{m^{4}}{l^{4}} - \frac{6}{l^{4}} - \frac{2}{l^{6}}) |
crystal structure of fluorine and methyl modified collagen: 2 (mepflpgly)7 |
 |
 |
=m^{4} \left(\frac{1}{l^{4}} - \frac{1}{l^{6}}\right) + m^{2} \left(- \frac{3}{l^{4}} + \frac{3}{l^{6}} + \frac{1}{l^{8}}\right) + \frac{1}{m^{2}} \left(\frac{1}{l^{6}} + \frac{2}{l^{8}} + \frac{1}{l^{10}}\right) + \frac{1}{l^{4}} - \frac{2}{l^{6}} - \frac{3}{l^{8}}) |
crystal structure of human apolipoprotein a-i |
 |
 |
=- 2 l^{6} - l^{4} m^{4} - 6 l^{4} - 4 l^{2} + m^{2} \left(l^{6} + 4 l^{4} + 2 l^{2}\right) + \frac{1}{m^{2}} \left(l^{6} + 2 l^{4} + l^{2}\right)) |
crystal structure of human apolipoprotein a-i |
 |
 |
=- l^{4} + l^{2} m^{4} + m^{2} \left(- l^{4} - 2 l^{2} - 1\right) + 1 + \frac{1}{m^{2}} \left(l^{6} + 2 l^{4} + l^{2}\right)) |
gramicidin a/cscl complex, active as a dimer |
 |
 |
=m^{2} \left(\frac{2}{l^{2}} + \frac{3}{l^{4}} + \frac{1}{l^{6}}\right) + \frac{1}{m^{2}} \left(\frac{1}{l^{2}} + \frac{2}{l^{4}} + \frac{1}{l^{6}}\right) - \frac{3}{l^{2}} - \frac{m^{4}}{l^{4}} - \frac{4}{l^{4}} - \frac{1}{l^{6}}) |
crystal structure of fluorine and methyl modified collagen: 2 (mepflpgly)7 |
 |
 |
=m^{2} \left(\frac{2}{l^{2}} + \frac{3}{l^{4}} + \frac{1}{l^{6}}\right) + \frac{1}{m^{2}} \left(\frac{1}{l^{2}} + \frac{2}{l^{4}} + \frac{1}{l^{6}}\right) - \frac{3}{l^{2}} - \frac{m^{4}}{l^{4}} - \frac{4}{l^{4}} - \frac{1}{l^{6}}) |
refinement of the influenza virus hemagglutinin by simulated annealing |
 |
 |
=m^{2} \left(\frac{2}{l^{2}} + \frac{3}{l^{4}} + \frac{1}{l^{6}}\right) + \frac{1}{m^{2}} \left(\frac{1}{l^{2}} + \frac{2}{l^{4}} + \frac{1}{l^{6}}\right) - \frac{3}{l^{2}} - \frac{m^{4}}{l^{4}} - \frac{4}{l^{4}} - \frac{1}{l^{6}}) |
crystal structure of e. coli nadp dependent enzyme |
 |
 |
=- l^{12} - 11 l^{10} - 21 l^{8} - 11 l^{6} + m^{6} \left(l^{8} + l^{6}\right) + m^{4} \left(- l^{10} - 8 l^{8} - 7 l^{6}\right) + m^{2} \left(6 l^{10} + 21 l^{8} + 15 l^{6}\right) + \frac{1}{m^{2}} \left(2 l^{12} + 7 l^{10} + 8 l^{8} + 3 l^{6}\right)) |
crystal structure of blub-like flavoprotein (yp_001089088.1) from 2 clostridium difficile 630 at 1.74 a resolution |
Solomon.1 # Hopf.2
 |
 |
=2 l^{6} + l^{4} - l^{2} + m^{2} \left(- l^{4} + l^{2}\right) + \frac{1}{m^{2}} \left(- l^{8} - 2 l^{6} - l^{4}\right)) |
gramicidin a/cscl complex, active as a dimer |
Solomon.2 # Hopf.1
 |
 |
=m^{2} \left(- \frac{4}{l^{4}} - \frac{2}{l^{6}}\right) + \frac{1}{m^{2}} \left(- \frac{1}{l^{4}} - \frac{2}{l^{6}} - \frac{1}{l^{8}}\right) + \frac{m^{4}}{l^{4}} + \frac{4}{l^{4}} + \frac{5}{l^{6}} + \frac{1}{l^{8}}) |
crystal structure of fluorine and methyl modified collagen: 2 (mepflpgly)7 |
Solomon.2 # Hopf.2
 |
 |
=m^{2} \left(-1 - \frac{4}{l^{2}} - \frac{1}{l^{4}}\right) + 3 + \frac{1}{m^{2}} \left(-1 - \frac{2}{l^{2}} - \frac{1}{l^{4}}\right) + \frac{m^{4}}{l^{2}} + \frac{5}{l^{2}} + \frac{2}{l^{4}}) |
coiled-coil domain of tumor susceptibility gene 101 |
Solomon.2 U Ring
 |
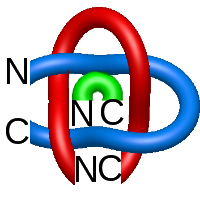 |
=m^{2} \left(\frac{1}{l^{2}} + \frac{1}{l^{4}}\right) + \frac{1}{m^{2}} \left(\frac{1}{l^{2}} + \frac{2}{l^{4}} + \frac{1}{l^{6}}\right) - \frac{3}{l^{2}} - \frac{4}{l^{4}} - \frac{1}{l^{6}}) |
an alpha/beta-peptide helix bundle with a pure beta-amino 2 acid core and a distinctive quaternary structure: gcn4pli 3 derivative with beta residues at a and d heptad positions |
Solomon.3 # Hopf.1
 |
 |
=m^{2} \left(\frac{1}{l^{2}} - \frac{1}{l^{4}}\right) + \frac{1}{m^{2}} \left(- \frac{1}{l^{4}} - \frac{2}{l^{6}} - \frac{1}{l^{8}}\right) - \frac{1}{l^{2}} + \frac{1}{l^{4}} + \frac{2}{l^{6}}) |
refinement of the influenza virus hemagglutinin by simulated annealing |
Solomon.4 # Hopf.1
 |
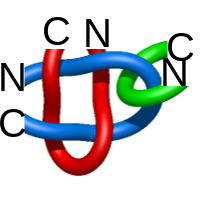 |
=2 l^{4} + l^{2} m^{4} + 5 l^{2} + m^{2} \left(- l^{4} - 4 l^{2} - 1\right) + 3 + \frac{1}{m^{2}} \left(- l^{4} - 2 l^{2} - 1\right)) |
cystal structure of rhesus macaque mhc class i:mamu-a*02 |
Solomon.4 # Hopf.2
 |
 |
=l^{8} + 5 l^{6} + l^{4} m^{4} + 4 l^{4} + m^{2} \left(- 2 l^{6} - 4 l^{4}\right) + \frac{1}{m^{2}} \left(- l^{8} - 2 l^{6} - l^{4}\right)) |
poliovirus late rna-release intermediate |
Star of David.1 U Ring
 |
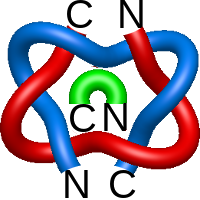 |
=m^{4} \left(\frac{1}{l^{4}} + \frac{1}{l^{6}}\right) + m^{2} \left(- \frac{5}{l^{4}} - \frac{6}{l^{6}} - \frac{1}{l^{8}}\right) + \frac{1}{m^{2}} \left(- \frac{1}{l^{4}} - \frac{2}{l^{6}} - \frac{1}{l^{8}}\right) + \frac{6}{l^{4}} + \frac{9}{l^{6}} + \frac{3}{l^{8}}) |
refinement of the influenza virus hemagglutinin by simulated annealing |
Star of David.2 U Ring
 |
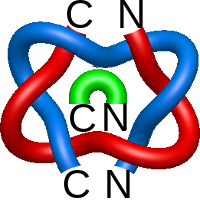 |
=l^{6} + 1 + \frac{1}{m^{2}} \left(- l^{8} - 2 l^{6} - l^{4}\right)) |
ribonuclease inhibitor-angiogenin complex |
Star of David.3 U Ring
 |
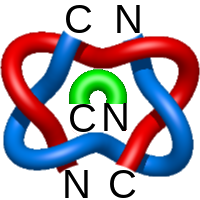 |
=3 l^{8} + 9 l^{6} + 6 l^{4} + m^{4} \left(l^{6} + l^{4}\right) + m^{2} \left(- l^{8} - 6 l^{6} - 5 l^{4}\right) + \frac{1}{m^{2}} \left(- l^{8} - 2 l^{6} - l^{4}\right)) |
poliovirus late rna-release intermediate |
Star of David.4 U Ring
 |
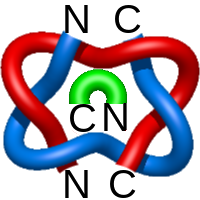 |
=1 + \frac{1}{m^{2}} \left(- \frac{1}{l^{4}} - \frac{2}{l^{6}} - \frac{1}{l^{8}}\right) + \frac{1}{l^{6}}) |
copper amine oxidase from hansenula polymorpha |
Whitehead.1 U Ring
 |
 |
=- l^{2} + m^{2} \left(1 + \frac{1}{l^{2}}\right) - 3 + \frac{1}{m^{2}} \left(l^{2} + 2 + \frac{1}{l^{2}}\right) - \frac{3}{l^{2}} - \frac{1}{l^{4}}) |
betaine aldehyde dehydrogenase from cod liver |
Whitehead.2 U Ring
 |
 |
=- l^{4} - 3 l^{2} + m^{2} \left(l^{2} + 1\right) - 3 + \frac{1}{m^{2}} \left(l^{2} + 2 + \frac{1}{l^{2}}\right) - \frac{1}{l^{2}}) |
poliovirus late rna-release intermediate |
Four-component links
Show observed structures with less then 10% probability.
Six and seven component links
Tab. 4 The five and six component macromolecular links.
[1] Dabrowski-Tumanski, P., Niemyska, W., & Sulkowska , J. I.
Are there links in proteins?
[2] Boutz, D. R., Cascio, D., Whitelegge, J., Perry, L. J., & Yeates, T. O. (2007).
Discovery of a thermophilic protein complex stabilized by topologically interlinked chains. Journal of molecular biology, 368(5), 1332-1344.
[3] Dabrowski-Tumanski, P., Niemyska, W., Pasznik, P., & Sulkowska, J. I. (2016).
LassoProt: server to analyze biopolymers with lassos. Nucleic acids research, gkw308.
[4] Sulkowska, J. I., Rawdon, E. J., Millett, K. C., Onuchic, J. N., & Stasiak, A. (2012).
Conservation of complex knotting and slipknotting patterns in proteins. Proceedings of the National Academy of Sciences, 109(26), E1715-E1723.
[5] Zhang, X., Guo, H., Jin, L., Czornyj, E., Hodes, A., Hui, W. H., ... & Zhou, Z. H. (2013).
A new topology of the HK97-like fold revealed in Bordetella bacteriophage by cryoEM at 3.5 Å resolution. Elife, 2, e01299.
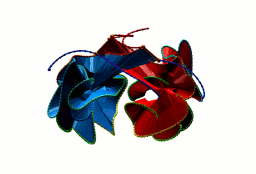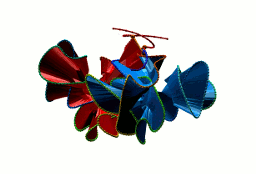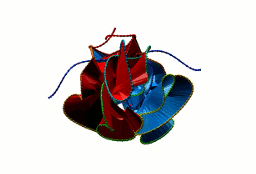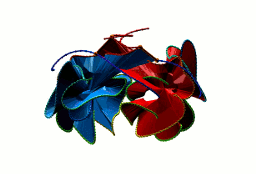
) and Solomon (
) links. As the protein chain is naturally oriented from the N- to the C-terminus, the links formed by covalent loops are equipped with an inherited orientation. This, orientation in principle, splits the topological types into smaller, topologically distinct subgroups. In particular, in the case of one-chain links, one can distinguish three topological types: positive Hopf link, negative Hopf link, and negative Solomon link (Fig. 1). The Hopf link and the Solomon links are prime links found in the mathematical enumeration of links, while the composition (or connected sum) of the Solomon link and the Hopf link is not shown in the enumeration since the tables only list prime knots/links.
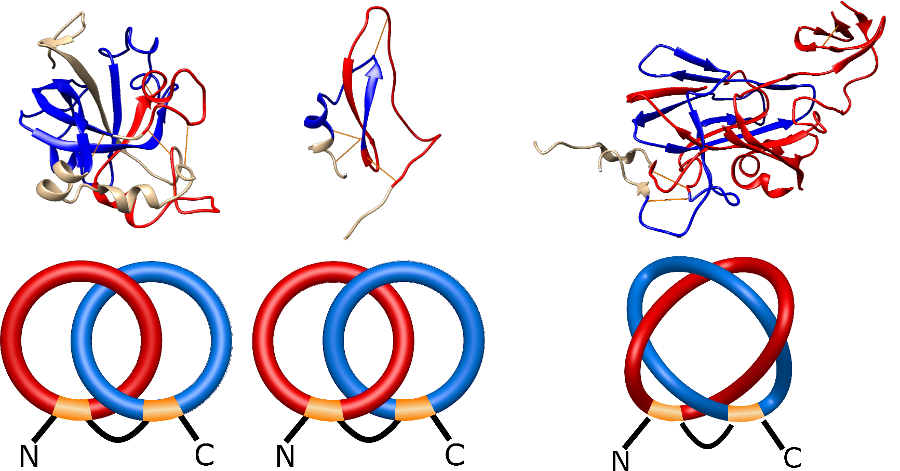



 ), the
), the link (
 ), in which each two components form the Hopf link, and a Hopf link with a split circle (
), in which each two components form the Hopf link, and a Hopf link with a split circle ( ). Such structures are presented in Tab. 2. All the probabilistic links are treated in the same manner as deterministic links for each chain termini connection. In particular, for each termini connection, the LinkProt database assigns a (triangulated) minimal surface and counts its piercings (Fig. 4).
). Such structures are presented in Tab. 2. All the probabilistic links are treated in the same manner as deterministic links for each chain termini connection. In particular, for each termini connection, the LinkProt database assigns a (triangulated) minimal surface and counts its piercings (Fig. 4).

















