Mathematically, links are the realization of a collection of circles in three dimensional Euclidean space. They are often oriented, i.e. each circle is provided with a direction called its orientation and the spatial realization is called an oriented link. The orientation is biologically relevant, as the protein chains are oriented from the N- to C-terminus. At the coarsest level, links are classified by the number of circles, the number of components, with the case of a single circle being called a knot. As in the case of knots, the proper, mathematical link is defined only for the closed loops. The LinkProt database distinguishes between three kinds of loop-closing definitions, resulting in three link types, described in detail below:
The collections of links of n components are next separated according to the number of crossings that appear in a generic orthogonal projection of the given link to a two dimensional plane with the smallest number of crossings. A generic projection is one whose crossing information is unchanged under small changes of projection direction implying that there are no vertical tangencies in the components, there are no triple crossings and, the tangent directions at double crossings are not collinear. Such projections are called knot or link presentations. These minimal crossing presentations are factored into connected sums with those that cannot be further factored into non-trivial summands being designated as prime, or irreducible, knots or links. The classification of links is the unique (each topologically equivalent link, up to mirror reflection, appears exactly once) identification of prime links of n components ordered by the minimal number of crossings and, within the collection of fixed minimal crossing number presentations, with the alternating presentations (those in which the crossings alternate between over and under when traversing each individual component of the link) followed by those that are not alternating. Finally, within each subcollection, individual links are ordered according to historical practice, e.g. the Alexander-Briggs table, or, in more contemporary listings, according to a facet of their symbolic coding, e.g. the Dowker-Thistlethwaite code with the 'alphabetical' ordering.
For each n component link, there may be as many as 2n+1 oriented links varying by mirror reflection (and the chirality of the link) and the orientation of the individual components. The result is that the identification of an m crossing n-component link quickly becomes a very challenging problem. In practice, there are small series of steps that one can take to achieve this identification:
Mathematical knots and links are classified according to minimal number of crossings in a two-dimensional projection of the knot or link. One of the problems of knot theory is to determine, if the knot or link in a given projection is mathematically equivalent (ambient isotopic) to a knot or link in another projection. The groundbreaking approach to this problem was to introduce the so-called knot polynomials. Every knot or link can be prescribed a polynomial which is invariant in different knot/link 2D projections. An important example of a general link polynomial is called HOMFLY-PT polynomial. It can be shown, that with appropriate substitution of variables, the HOMFLY-PT polynomial can be turned into well-known Alexander or Jones polynomial. The HOMFLY-PT polynomial in its original form is defined as a three-variable polynomial fullfiling the Skein relation [1]:
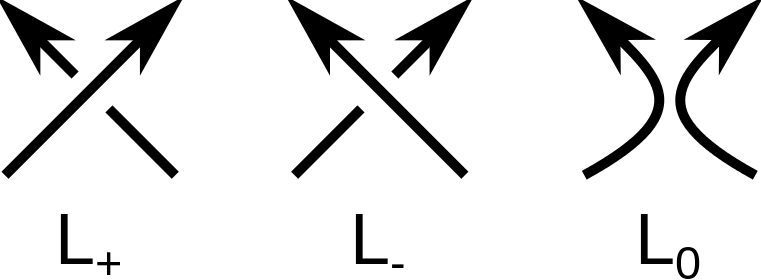
Where denotes the unknot (the trivial knot), and
,
and
knot or link diagrams differing in orientation of only one crossing as in the picture on the right hand side.
As from the definition the HOMFLY-PT polynomial is homogenous, it can be presented in the two-variable form. Different representations of HOMFLY polynomial are common. In LinkProt we use the relation . Note, that in Mathematica the relation is
, while in katlas the relation is
. To calculate the HOMFLY-PT polynomial for a given closed loop we use the implementation of the polynomial of Ewing and Millet [4].
In mathematics and science, a structure or object is chiral if one can distinguish it from its mirror reflection as is the case for the left and right hands. One imagines the two hands placed palm to palm with an imaginary mirror between them indicating the result of a reflection. In the case of the mathematical study of knots and links, early researchers’ classifications did not distinguish between mirror reflections. Thus, the right and left handed trefoils where known simply as the trefoil. In contemporary mathematics and science, it is understood that the two trefoils are indeed different and, depending on the setting, one may be preferred over the other. Not all knots or links are chiral. For example, the Hopf link or the figure-eight knot are both examples of achiral structures, i.e. they are topologically indistinguishable from their mirror images.
As, for some purposes, the specific chiral structure is important while, in other cases, it is not important, we have included a feature that allows one to void the chiral distinction between structures and focus attention on other facets such as the number of components or the complexity as measured by crossing number or the topological type of the configuration. In particular, the user can choose to display only e.g. the Hopf link structures, regardless of the orientation of the components (see Search and browse database). Nevertheless, the statistics given on the bottom of the page include the chirality and orientation of molecules. To display the statistics regardless of the chirality, we provide the "Disregard chirality" button in the top of the page.
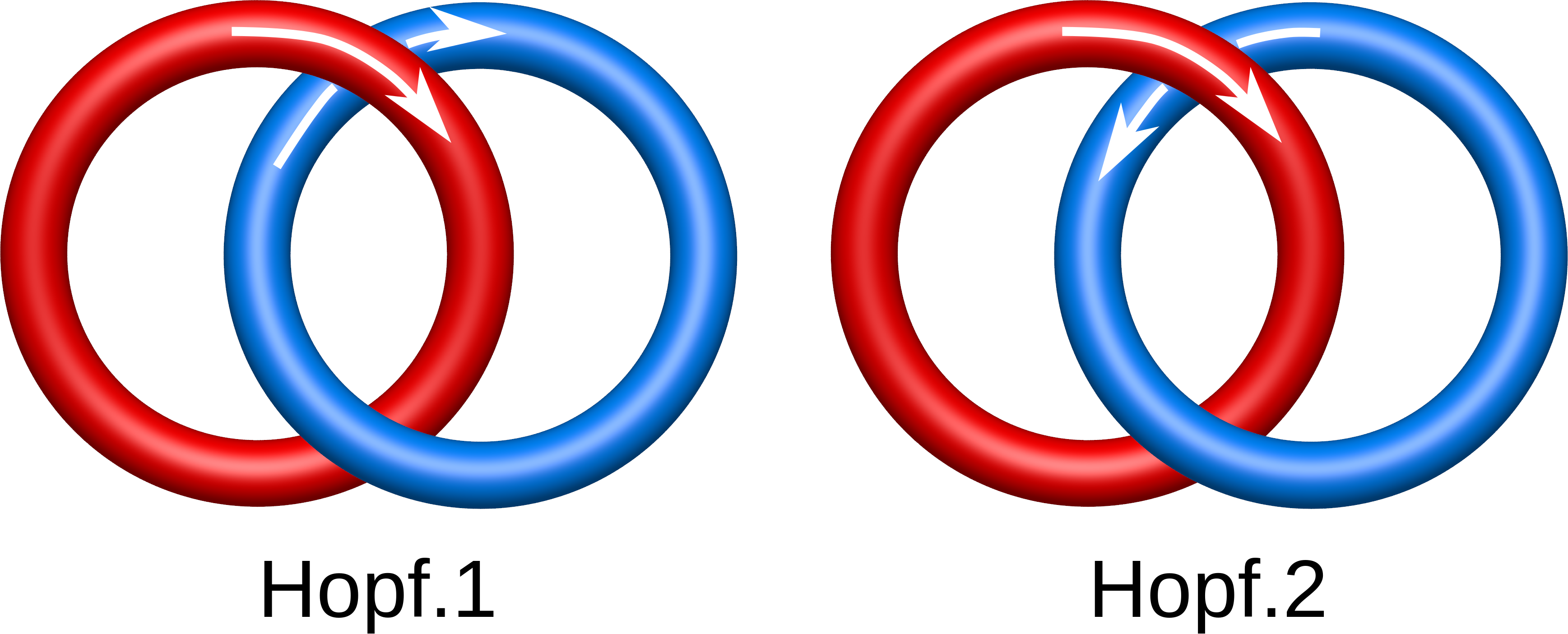
Fig. 1 Different Hopf links, taking into account the orientation.
The chirality and sensitivity to orientation change splits the link topological classes into smaller subclasses. In particular, there are two Hopf links differing in the orientation only (Fig. 1). On the other hand some chiral links (like the Solomon link) need also to be distinguished from their mirror image (Fig. 2). In LinkProt, for each subclass arbitrary number is prescribed. Therefore, e.g. the Solomon link class is constituted by Solomon.1, Solomon.2, Solomon.3 and Solmon.4 subclasses (Fig. 2). In the main Search page only the main classes are presented, but clicking on the "Details" button allows to select also the desired subclasses (see Search and browse database).
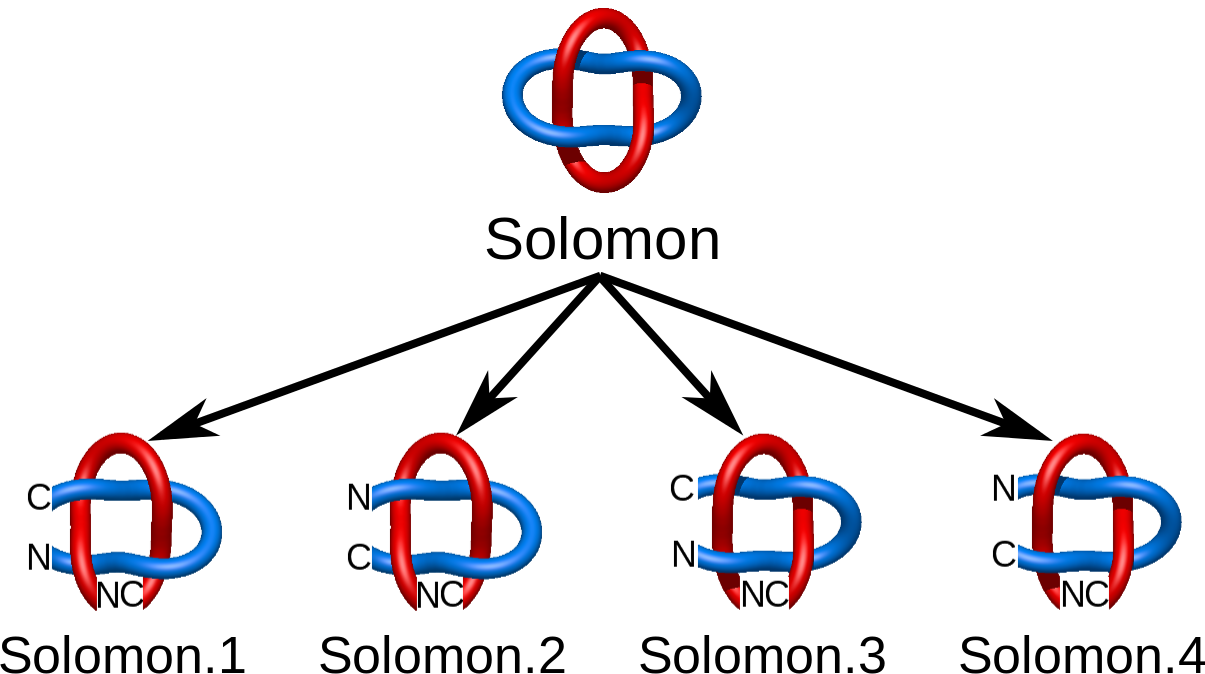
Fig. 2 Four different Solomon links taking into account chirality and chain orientation.
The minimal surface analysis follows the algorithm proposed in [2,3] and used in the LassoProt server and database. For each closed loop we prescribe the triangulation of a minimal surface, which allows us to define piercing through the loop. This is an alternative description of the linking, revealing potentially important residues from a biological perspective. The surface is constructed based on the positions of Cα atoms (the vertices), on which the initial mesh of triangles is built. Subsequently, the triangles are divided, swapped and optimized to achieve the triangulation with minimal area (Fig. 3). We should note however, that the surface obtained is the local area minimum, and there can be other surfaces with lower total area. However, this have not hindered our calculations for the entire RCSB database.
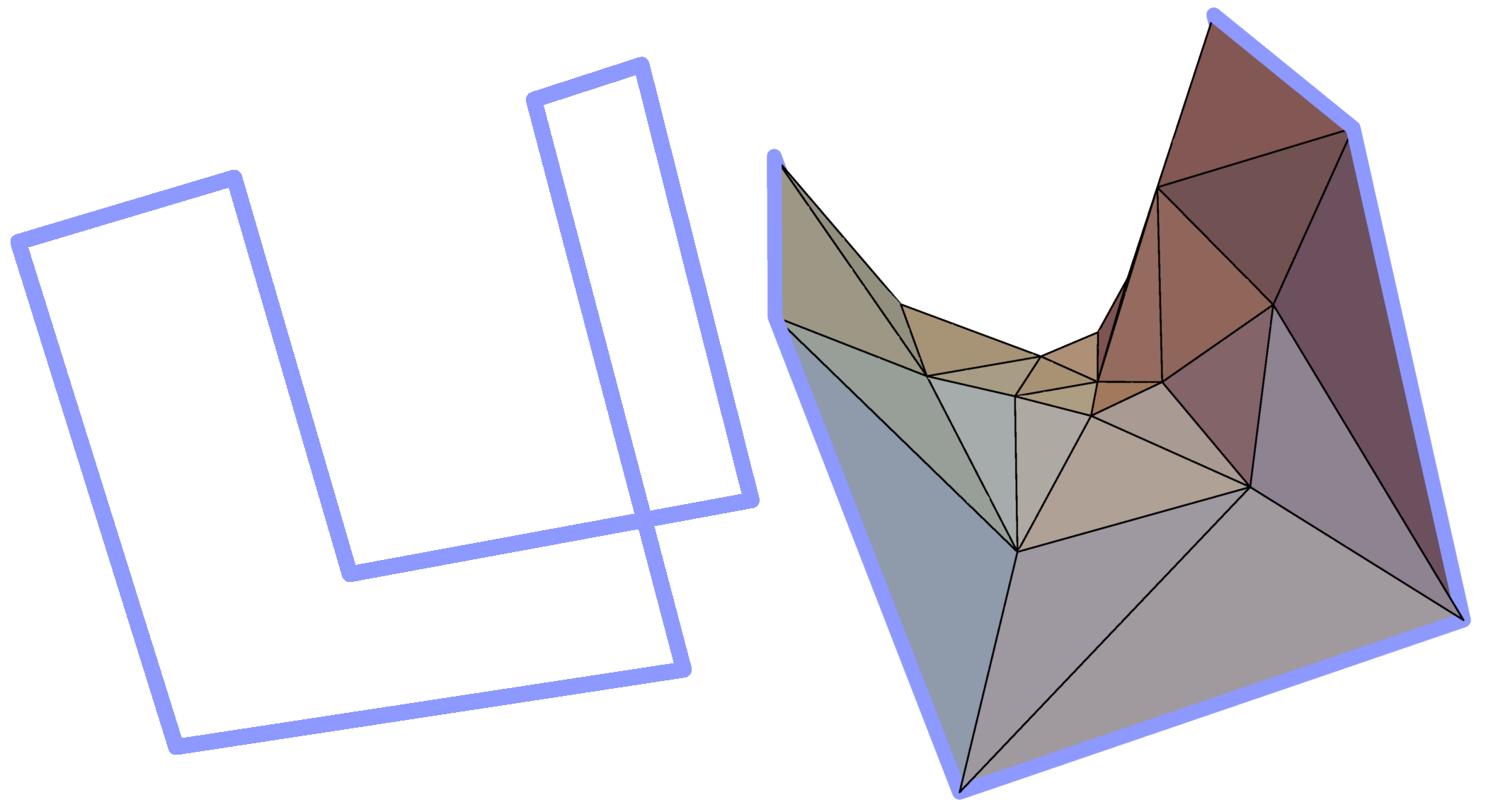
Fig. 3 Example of a simple polygon in three-dimensional space (left panel) and a triangulated minimal surface spanning it (right panel).

Fig. 4 Surfaces spanning the covalent loops of beta-expansin with PDB code 2HCZ - left and right panel - single surfaces, middle panel - both surfaces together.
The deterministic links arise in the proteins with covalent bonds joining the protein sidechains (e.g. disulfide bonds). Such bonds naturally determine the covalent loop in the protein chain. If the loop is pierced by the other portion of the chain, the structure is called the complex lasso protein. The complex lasso proteins were studied in [2] and the database LassoProt collects information about such proteins. From this perspective the link structure can be viewed as the protein containing two interlocking complex lasso motifs.
Probabilistic links arise in multichain models upon joining the termini of each chain. Similar technique was introduced earlier to define the knots in proteins, however in that case the termini of only one chain were joined [5]. There are a few techniques, how the termini could be joined. The simple method to connect the termini directly can introduce additional crossing of the chain in its projection on 2D plane, changing artificially its link type. Therefore the termini are expanded towards the large sphere and then joined on the sphere (Fig. 5). In general, the type of the link depends on the direction of expansion. Therefore one can talk about the probability of obtaining a link in the set of all possible closures. The probability of each link is depicted as a circle plot in the default view of each protein (see Search and browse database).
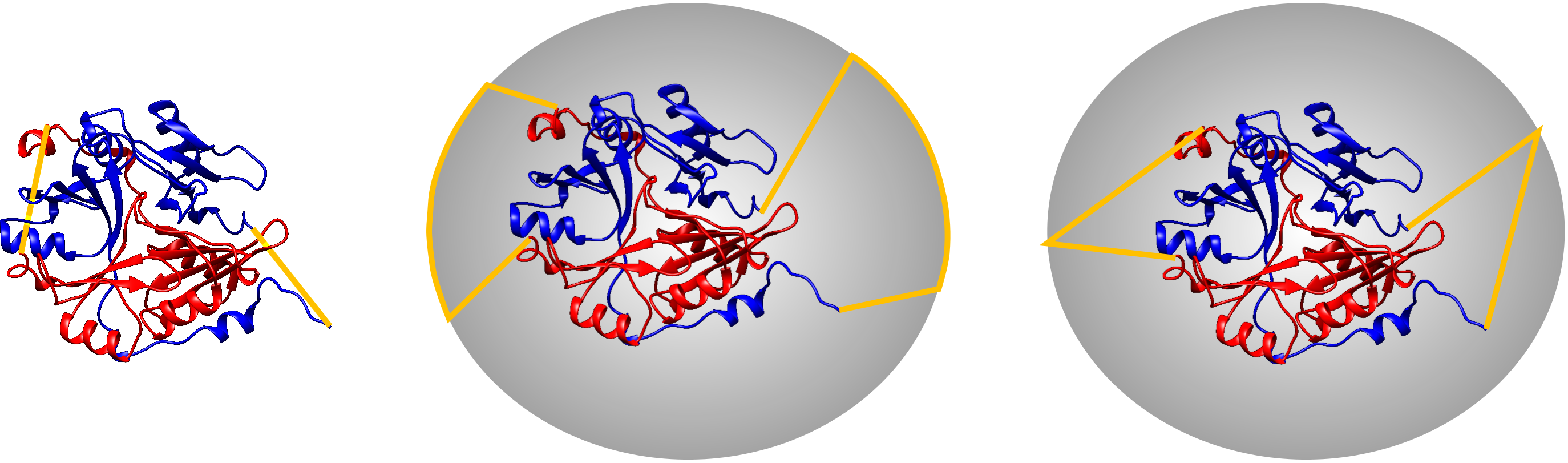
Fig. 5 Different chain termini connection methods for the same protein. Left panel - direct connection of the termini introducing additional crossing, middle panel - connection on the sphere with the use of two points, right panel - connection of the sphere with the use of one point. The chains are depicted red and blue, the connecting interval is depicted with the orange strips.
In knot detection one usually uses the method of expanding the termini towards two distinct points on the sphere, and the termini are joined by joining both points on the sphere. In the case of links, the intervals joining points on the sphere can also cross changing artificially the topology. Therefore in LinkProt database we use the technique with only one point on the sphere (Fig. 4 right panel).
The third type of links stored in the LinkProt database are the macromolecular links. In such cases, the components of the link are formed by several chains, not by one chain, or part of the chain as it was in probabilistic or deterministic links. In such a case the components are formed either by connecting the chains' termini with straight interval, or by the covalent link between the chains. Macromolecular links often arise in bacteriophages or in virus capsids, introducing additional stabilization of the whole structure (see Application section).